Анализ данных эксперимента

Рассмотрим некоторый эксперимент, в ходе которого в моменты времени

< <... <

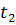производится, например, измерение температуры Q(t). Пусть результаты измерений задаются массивом

, ,..., .

Допустим, что условия проведения эксперимента таковы, что измерения проводятся с заведомой погрешностью. В этих случаях закон изменения температуры Q(t) ищут с помощью некоторого полинома

P(t) = + + +... + ,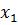

определяя неизвестные коэффициенты 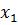, ,..., из тех соображений, чтобы величина E(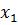,..., ), определяемая равенством

E (,..., ) =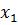

принимала минимальное значение. Поскольку минимизируется сумма квадратов, то этот метод называется аппроксимацией данных методом наименьших квадратов.

Если заменить P(t) его выражением, то получим

=

Поставим задачу определения массива так, чтобы величина была минимальна, т.е. определим массив методом наименьших квадратов. Для этого приравняем частные производные по к нулю:

Если ввести m × n матрицу A = (), i = 1, 2..., m; j = 1, 2,..., n, где

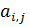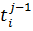= , i = 1, 2..., m; j = 1, 2,..., n,

то выписанное равенство примет вид

(k=1,2,…,n)

или

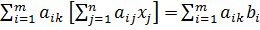(k=1,2,…,n)

Перепишем написанное равенство в терминах операций с матрицами. Имеем по определению умножения матрицы на столбец

Для транспонированной матрицы аналогичное соотношение выглядит так

Введем обозначение: i –ую компоненту вектора Ax будем обозначать В соответствии с выписанными матричными равенствами будем иметь

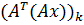= (k=1,2,…,n)

В матричной форме это равенство перепишется в виде

A^T x =A^TB (1.3)

Здесь A – прямоугольная m× n матрица. Причем в задачах аппроксимации данных, как правило, m > n. Уравнение (1.3) называется нормальным уравнением.

Можно было с самого начала, используя евклидову норму векторов, записать задачу в эквивалентной матричной форме:

= =

=

Наша цель минимизировать эту функцию по x. Для того чтобы в точке решения достигался минимум, первые производные по x в этой точке должны равняться нулю. Производные данной функции составляют

− 2A^T B + 2A^TAx

и поэтому решение должно удовлетворять системе линейных уравнений

(A^TA)x = (A^TB).

Эти уравнения называются нормальными уравнениями. Если A – m× n матрица, то A>A – n × n - матрица, т.е. матрица нормального уравнения всегда квадратная симметричная матрица. Более того, она обладает свойством положительной определенности в том смысле, что (A>Ax, x) = (Ax, Ax) ≥ 0.

Замечание. Иногда решение уравнения вида (1.3) называют решением систе- мы Ax = b, где A прямоугольная m × n (m > n) матрица методом наименьших квадратов.

Задачу наименьших квадратов можно графически интерпретировать как минимизацию вертикальных расстояний от точек данных до модельной кривой (см. рис.1.1). Эта идея основана на предположении, что все ошибки в аппроксимации соответствуют ошибкам в наблюдениях . Если имеются также ошибки в независимых переменных , то может оказаться более уместным минимизировать евклидово расстояние от данных до модели.

рис.1.1.

Дата добавления: 2015-08-20