Метод Гаусса.

Алгоритм Метода Гаусса состоит из двух основных частей: прямой ход и обратный ход.

Прямой ход заключается в том, что система приводится к треугольному виду (верхняя унитреугольная форма). Обратный ход-непосредственное нахождение неизвестных. Причем, корни находятся в обратном порядке: сначала , затем 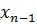и т.д.

1) Прямой ход состоит из следующих шагов.

На первом шаге элементарными преобразованиями исключается 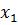из всех уравнений, начиная со второго.

Второй шаг заключается в исключение из всех уравнений, начиная с третьего.

На s шаге исключается из всех уравнений, начиная с s+1

(s=1,…,n-1).

При этом каждый шаг начинается с обработки s уравнения: строка под номером s делится на ,чтобы коэффициент при стал равен 1.

Описанный алгоритм носит циклический характер.

После завершения этого процесса получаем систему:

(2)

2) Обратный ход. В результате выполнения алгоритма прямого хода система (1) приняла треугольный вид (2). Для нахождения решения остается из системы (2) найти 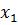, , …, . Метод нахождения достаточно очевиден: из последнего уравнения находим .

Затем, подставив найденное значение в (n-1)-ое уравнение, найдем 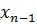, и т.д. Таким образом, s-ое неизвестное находим из s-го уравнения:

. 1.0.

Причем, если условиться считать, что значение суммы, в которой нижний индекс суммирования больше верхнего (пустая сумма), равно нулю, в формуле 1.0. можно считать, что индекс s принимает натуральные значения от n до 1.

Дата добавления: 2015-08-20