В общем виде задача линейного программирования ставится следующим образом.

Максимизировать (минимизировать) функцию

(3.1)

при ограничениях

где x_j, –управляющие переменные или решения задачи
(3.1)–(3.4); b_j, a_ij, – параметры, f – целевая функция или критерий эффективности задачи.

Функция (3.1) – линейная, ограничения (3.2)–(3.4) – линейные. Задача содержит п переменных и т ограничений.

Каноническая и симметрическая форма злп 2. Каноническая форма записи задачи линейного программирования: необходимо найти экстремальное значение целевой функции (4.1) при ограничениях

На все неизвестные наложены условия неотрицательности:

3. Симметричная форма записи задачи линейного программирования. Здесь принято выделять две стандартные задачи − задачу максимизации и задачу минимизации.

3.1. Стандартная задача максимизации: необходимо найти максимальное значение целевой функции (4.1) при ограничениях

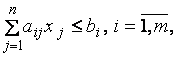
и условиях неотрицательности (4.2).

3.2. Стандартная задача минимизации: необходимо найти минимальное значение целевой функции (4.1) при ограничениях

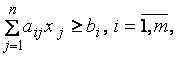
и условиях неотрицательности

Дата добавления: 2015-08-20