Читайте также:
|
· Если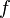 
есть аналитическая функция в любой точке 
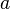, то её ряд Тейлора в любой точке 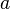области определения 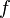сходится к 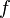в некоторой окрестности .
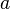· Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности 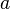. Коши предложил такой пример:
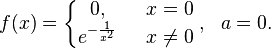
У этой функции все производные в нуле равны нулю, поэтому коэффициенты ряда Тейлора в точке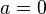 
равны нулю.
Дата добавления: 2015-08-20; просмотров: 48 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Определение | | | Различные формы остаточного члена |