Читайте также:
|
Пусть функция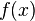 
бесконечно дифференцируема в некоторой окрестности точки 
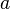. Формальный ряд
называется рядом Тейлора функции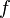 
в точке .
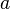То есть, рядом Тейлора для функции 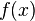в окрестности точки 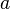называется степенной ряд относительно двучлена 
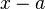вида 
Дата добавления: 2015-08-20; просмотров: 49 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Понятие суммы степенного ряда. Ряд Тейлора | | | Свойства |