Читайте также:
|
Фундаментальная система решений – это множество линейно независимых векторов 
, каждый из которых является решением однородной системы, кроме того, решением также является линейная комбинация данных векторов 
, где 
– произвольные действительные числа.
Количество векторов 
фундаментальной системы рассчитывается по формуле:
Однако в практических заданиях гораздо удобнее ориентироваться на следующий признак: количество векторов фундаментальной системы равно количеству свободных неизвестных.
Представим общее решение Примера №3 
в векторной форме. Свободная переменная в данном случае одна, поэтому фундаментальная система решений состоит из единственного вектора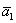 
. Как его найти? Для этого свободной переменной нужно придать произвольное ненулевое значение. Проще всего, конечно же, выбрать 
и получить: 
.
Координаты вектора 
должны удовлетворять каждому уравнению системы, и будет не лишним в этом убедиться.
Ответ следует записать в виде линейной комбинации векторов фундаментальной системы. В нашей ситуации линейная комбинация состоит из одинокого слагаемого. Общее решение однородной системы я буду обозначать через вектор 
(подстрочный индекс расшифровывается «Общее Однородной»).
Ответ: общее решение: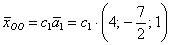 
, где 
(любое вещественное число)
Придавая параметру 
различные действительные значения, можно получить бесконечно много частных решений, например, если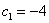 
, то вектор частного решения однородного уравнения («Частное Однородной») равен:
, то есть набор переменных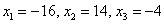 
удовлетворяет каждому уравнению системы.
Это мы рассмотрели традиционный способ построения фундаментальной системы в так называемом нормальном виде – когда свободным переменным придаются исключительно единичные значения. Но правила хорошего математического тона предписывают избавляться от дробей, если это возможно. Поэтому в данном случае можно взять 
и из общего решения системы получить вектор с целыми координатами: 
И тогда ответ запишется в эквивалентной форме:
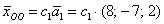, где (любое вещественное число)
Дата добавления: 2015-08-18; просмотров: 49 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Свойства линейных однородных дифференциальных уравнений. | | | Однородные системы линейных уравнений |