
Читайте также:
|
Здійснити планування рандомізованого експерименту за наступними вхідними даними:
Результати досліджень тиску р, навколишньої температури t, концентрації окислів с в окислювальному середовищі роботи термопари, функцією відклику яких є планована в результаті експерименту додаткова похибка при подальших незалежних змінах впливаючих факторів подані в табл.3.2. Знайти та дати кількісну характеристику впливовості кожного із зазначених факторів із застосуванням латинського(греко-латинського) квадрату.
Примітка: значення додаткової похибки аналогічні до наведеного прикладу у теоретичній частині.
Таблиця 3.2 - Впливаючі фактори на додаткову похибку термопари.
| р, атм. | ||||
| г,°С | ||||
| с,% |
Розв’язок. При організації даного експерименту і при рандомізації впливаючих факторів (табл. 3.2) необхідно виконати певні застереження щодо можливого руйнування засобу вимірювання у заданому агресивному середовищі. Зокрема, надмірний тиск, висока температура та підвищена концентрація окислів в агресивному середовищі може призвести до виходу додаткової похибки за межі допустимої або навіть до руйнування термопари.
Матрицю планування побудуємо у вигляді латинського квадрата 4x4 (табл. 3.4).
Таблиця 3.4 - Матриця планування (латинський квадрат 4x4)
| Тиск р, атм. | Температур t°C | |||
| с=16 | с=20 | с=14 | с=15 | |
| с=15 | с=16 | с=20 | с=14 | |
| с=14 | с=15 | с=16 | с=20 | |
| с=20 | с=14 | с=15 | с=16 |
Після поставлення експерименту за поданим планом отримані дані подамо як суміщену матрицю (табл. 3.5).
Таблиця 3.5 - Суміщена матриця за планом експерименту в координатах p-t
| p \ t | Tp- | ||||
| с=16 3,8 | с=20 3,7 | с=14 3,3 | с=15 3,6 | T1- = 14,4 | |
| с=15 3,3 | с=16 3,9 | с=20 4,3 | с=14 3,6 | T2- = 15,1 | |
| с=14 3,4 | с=15 3,7 | с=16 4,0 | с=20 4,4 | T3- = 15,5 | |
| с=20 4,2 | с=14 3,5 | С=15 3,9 | с=16 4,3 | T4- = 15,9 | |
| T-t | T-1 = 14,7 | T-2 = 14,8 | T-3 = 15,5 | T-4 = 15,9 | T-- |
У цій суміщеній матриці знайдена сума спостережень за факторами тиск та температура. Для знаходження суми спостережень за фактором концентрація змінимо координати матриці (табл. 3.6).
| с \ t | T-с- | ||||
| с=14 | с=14 3,4 | с=14 3,5 | с=14 3,3 | с=14 3,6 | T-1- = 13,8 |
| с=15 | с=15 3,3 | с=15 3,7 | с=15 3,9 | с=15 3,6 | T-2- = 14,5 |
| с=16 | с=16 3,8 | с=16 3,9 | с=16 4,0 | с=16 4,3 | T-3- = 16,0 |
| с=20 | с=20 4,2 | с=20 3,7 | с=20 4,3 | с=20 4,4 | T-4- = 16,6 |
| T-t | T-1 = 14,7 | T-2 = 14,8 | T-3 = 15,5 | T-4 = 15,9 | T-- |
Таблиця 3.6 - Суміщена матриця за планом експерименту в координатах c-t
Дисперсійний аналіз проводиться у наступній послідовності:
• загальна сума квадратів відхилень за експериментальними даними усіх дослідів (за усією таблицею) відносно загального середнього

• сума квадратів відхилень за р - фактором (тиск) від загального середнього

• сума квадратів відхилень за с-фактором (концентрація) від загального середнього

• сума квадратів відхилень за t-фактором (температура) від загального середнього

• сума квадратів похибки

Усі отримані результати дисперсійного аналізу подамо у вигляді результуючої матриці (табл. 3.7).
Таблиця 3.7 - Результуюча матриця
| Джерело впливу | Кількість ступенів свободи | Сума квадратів відхилень SS | Середній квадрат відхилень S2 | Перевірка Н0:
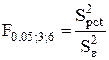
|
| Тиск | 0,307 | 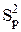 = 0,102 = 0,102
| 5,38 | |
| Концентрація | 1,262 |  = 0,421 = 0,421
| 22,16 | |
| Температура | 0,247 |  = 0,082 = 0,082
| 4,32 | |
| Похибка | 0.113 |  = 0.019 = 0.019
| - | |
| Сума | 1,929 | - | - |
Оскільки табличне значення коефіцієнта Фішера, що дорівнює F0.05;3;6=4,76 перевищує розраховане значення у табл.3.7 для температури, то можна зробити висновок про значущість впливу температури на додаткову похибку термопари.
Дата добавления: 2015-08-17; просмотров: 77 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Загальний розв'язок трифакторної задачі методомлатинського квадрата nхn | | | ЛИНГВИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ |