ЗАДАЧА 3. За даними двох незалежних вибірок обсягів m=18 і n=24 з нормальних генеральних

За даними двох незалежних вибірок обсягів m= 18 і n= 24 з нормальних генеральних сукупностей X і Y обчислені емпіричні дисперсії S 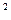(X) =9, 83 й S 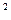(Y)=7, 54. Потрібно при рівні значимості α=0, 05 перевірити гіпотезу H: D(X) = D(Y) при альтернативній гіпотезі H1: D(X) > D(Y).

Розв’язок: Обчислимо по формулі (2.3) відношення більшої емпіричної дисперсії до меншого: F =9.83 / 7, 54=2,43.

По таблиці критичних точок розподілу Фішера-Снедекора при α=0, 05,

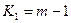=17, 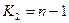=23 визначаємо 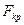 (0.05;17;23)=2,00.

Висновок: тут F > F 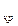тому, що значення відношень дисперсій більше критичного, то є підстави відкидати гіпотезу про рівність дисперсій.

Планування рандомізованих експериментів

Рандомізований експеримент - це такий експеримент, який передбачає випадковий характер проведення досліду чи груп дослідів.

Рандомізовані експерименти в постановці завдання та методах їх реалізації можна розподілити на такі основні класифікаційні групи:

• метод змішування факторів, що передбачає максимально можливу, але доцільну кількість реально впливаючих факторів;

• метод повноблочного збалансованого плану або метод додаткового досліду як метод, в якому встановлюються наперед задані обмеження;

• метод рандомізації за зовнішньою змінною як такий, в якому окремі досліди несуть конкретизоване, але різне змістовне навантаження;

• метод латинського квадрата або метод із строго обме­женою рандомізацією, коли окремі досліди є адекватними за своїм змістовним навантаженням;

• метод греко-латинського квадрата, як різновид латинського квадрата, в якому використовується додатковий (четвертий) впливаючий фактор.

Кожний із вказаних методів має свої особливості, які доцільно розглядати на конкретних прикладах. В даній курсовій роботі більш детально розглянуто метод латинського квадрата.

Дата добавления: 2015-08-17