Методи статистичної перевірки гіпотез

Статистичними гіпотезами називають гіпотези про вид невідомого закону розподілу або про параметри відомого розподілу, що перевіряють за результатами спостережень. Часто поряд з основною гіпотезою H розглядається конкуруюча (альтернативна) гіпотеза H1.

Помилкою першого роду називається помилка, яка полягає в тому, що відхиляється основна гіпотеза H, якщо насправді ця гіпотеза вірна.

Помилкою другого роду називається помилка, яка полягає в тому, що основна гіпотеза H приймається, хоча в дійсності вірна конкуруюча гіпотеза H1.

Для перевірки гіпотез будують статистичні критерії, які заключаються в тому, що за допомогою спеціально підібраної випадкової величини з відомим розподілом, визначають критичну область, при попаданні в яку вибірки x , x ,...x основна гіпотеза H відхиляється.

Критеріями згоди називають критерії перевірки про передбачуваний закон невідомого розподілу.

Рівнем значимості критерію називають імовірність помилки першого роду.

Потужністю критерію називають величину 1-β, де β − імовірність помилки другого роду.

У процесі досліджень часто виникає необхідність за емпіричним середнім і при заданому рівні значимості α перевірити гіпотезу H про

M (X) = M (Y) − рівності математичних очікувань двох нормальних розподілів з відомими дисперсіями.

Якщо і обчислені за незалежними вибірками, обсяги яких відповідно рівні m і n, можна довести, що випадкова величина

(2.1)

розподілена нормально з параметрами 0 і 1. Якщо конкуруюча гіпотеза H1 полягає в тому, що M(X)≠M(Y), то найбільш потужним критерій буде у разі симетричної критичної області: і . Границі області визначаються зі співвідношення:

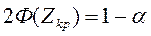(2.2)

Завдання такого типу виникають на виробництві при вибірковому контролі якості однакових типів виробів, виготовлених на різних верстатах або при різних технологічних режимах.

При порівнянні точності приладів, інструментів, технологічних процесів і при рішенні багатьох інших завдань виникає необхідність порівняння дисперсій.

Так, нехай випадкові величини X і Y розподілені нормально. За даними двох відповідних незалежних вибірок обсягів m і n обчислено виправлені дисперсії S 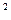(X) й S 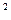(Y) Перевіримо гіпотезу H: D(X) = D(Y), щодо альтернативної гіпотези H1: D(X) > D(Y).

Можна довести, що відношення:

S 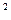(X)/ S 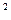(Y)= F (2.3)

більшої дисперсії до меншої при справедливості основної гіпотези не залежить від невідомих параметрів і має розподіл Фішера - Снедекора зі ступенями свободи і .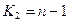

Тоді при заданому рівні значимості α по таблиці F − розподілу Фішера-Снедекора визначимо відповідне значення .

Якщо виявиться, що значення F відношення (2.3) дисперсій більше критичного, гіпотеза H відкидається; якщо спостережуване значення менше, або дорівнює критичному, то гіпотеза H приймається.

Дата добавления: 2015-08-17