ЗАДАЧА 1. Результати дослідження залежності об’єму досліджуваного газу Y від температури X для

Результати дослідження залежності об’єму досліджуваного газу Y від температури X для 166 рівноточних вимірювань наведені кореляційній таблиці

		Х
(X,Y)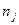
Y

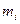
Потрібно:

1) побудувати емпіричну ламану регресії Y на X;

2) вибрати вид рівняння регресії;

3) оцінити залежність між Y і X емпіричним коефіцієнтом кореляції;

4) скласти емпіричне рівнянні регресії;

5) накреслити графік лінії регресії (у системі координат,

використовуваної для побудови емпіричної ламаної).

Розв’язок: 1) Для побудови емпіричної ламаної регресії Y на X обчислимо середнє значення об’єму досліджуваного газу при кожному значенні температури:

Потім наносимо точки на площину в системі координат X О Y і з'єднуємо їх відрізками прямих (рис.1).

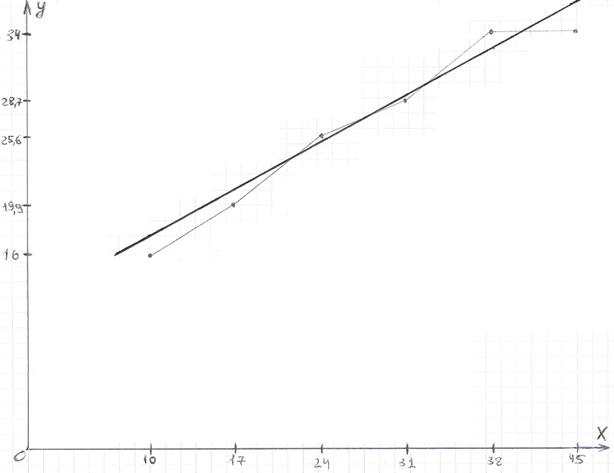
2) Розташування точок на площині ХО Y дозволяє припустити наявність прямолінійної кореляційної залежності між Y і X.

3) Обчислюємо коефіцієнт кореляції і параметри рівняння регресії:

Порівняно невелике значення r, яке за позначенням r [-1,1], підтверджує припущення про лінійну кореляційну залежність між Y і X.

4) Емпіричне рівняння регресії має вигляд: y= 0.55x+11.8.

5) Накреслимо графік лінії регресії (рис.1).

Взаємне розташування на рисунку емпіричної ламаної і емпіричної прямої регресії свідчить про те, що припущення про лінійну регресію згідно з результатами спостережень.

Аналітично це питання вирішується за допомогою перевірки гіпотези про значимість коефіцієнта кореляції.

Висновок: кореляційний зв‘язок прямий і тісний.

Дата добавления: 2015-08-17