Загальний розв'язок трифакторної задачі методомлатинського квадрата nхn

В основі загального розв’язку трифакторної задачі методом латинського квадрата nхn лежать такі засади:

· наявність трьох незалежних факторів: x_i, x_j, x_k;

· матриця планування на зразок латинського квадрата nхn;

· можливість переходу від матриці планування до матриці даних чи суміщеної матриці;

· лінійна математична модель

,

· яку знаходять за планом латинського квадрата з трьома x_i, x_j, x_k -факторами, кожний з яких має n-рівнів і, j i k;

· основне рівняння дисперсійного аналізу

.

Опрацювання результатів методом дисперсійного аналізу проводиться знаходженням:

· загальної суми квадратів відхилень за експериментальними даними усіх дослідів (за усією таблицею) відносно загального середнього ;

· суми квадратів відхилень за n i-их рівнів х_i.- фактора від загального середнього

· суми квадратів відхилень за n j-их рівнів х_j.- фактора від загального середнього

· суми квадратів відхилень за n k-их рівнів х_k.- фактора від загального середнього

· суми квадратів похибки, що знаходиться за формулою (3.5);

· дисперсій - за формулами (3.9);

· значущості - за критерієм Фішера.

Необхідно детальніше зупинитись на використанні нуль-гіпотези в статистичних висновках при розв'язку трифакторної задачі.

Гіпотеза в статистиці – це усяке твердження яке підлягає перевірці, то при розв'язку задачі з трьома впливаючими факторами перевірці підлягають здебільшого кілька гіпотез: Н₀, Н₁ Н₂,..., Н_і.

Проста гіпотеза підтверджує, що два незалежні спостереження (чи вимірювання) є різними. Такого змісту можуть набути три гіпотези в трифакторній задачі: Н₁₂, Н₁₃, Н₂₃.

Альтернативна простій гіпотезі є нуль-гіпотеза Н₀, яка вперше введена Фішером. Нуль-гіпотеза - це гіпотеза яка стверджує відсутність значущої різниці між результатами двох аналізів, спостережень, проведених розрахунків тощо. Для двох дисперсій запишемо:

Н₀: .

Перевірка нуль-гіпотези здійснюється порівнянням розрахованого критерію Фішера з його табличним значенням, а саме:

· коли гіпотеза підтверджується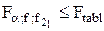

· коли гіпотеза не підтверджується

При вирішенні трифакторної задачі у висновку відзначають:

• вплив кожного з трьох факторів на параметр оптимізації чи функцію відклику;

• поділ впливаючих факторів за їх значущістю.

При загальному розв'язку трифакторної задачі методом латинського квадрата 4x4 після побудови матриці планування, матриці даних (суміщеної матриці) та знаходження відповідних сум спостережень для кожного з 12-ти рівнів (3 фактори, кожний на 4-х рівнях) матимемо:

• загальну суму квадратів відхилень за експериментальними даними усіх дослідів (за усією таблицею) відносно загального середнього

(3.1)

• суму квадратів відхилень за n=4 і-их рівнів х_і - фактора від загального середнього

; (3.2)

• суму квадратів відхилень за n=4 j-их рівнів х_j - фактора від загального середнього

; (3.3)

• суму квадратів відхилень за k=4 k-иx рівнів x_k- фактора від загального середнього

; (3.4)

• суму квадратів похибки, що знаходиться за формулою

(3.5)

з використанням (3.1), (3.2), (3.3) і (3.4);

• кількість ступенів свободи для кожного з факторів, для усіх дослідів та для похибки, що відповідно визначається як:

f_i = f_j = f_k = n – 1 = 4 – 1 = 3; (3.6)

(3.7)

(3.8)

• дисперсії чи середній квадрат кожного з розглянутих відхилень, що визначаються за формулами

; ; ; (3.9)

та даними (3.6)-(3.8) як:

; ; ; ; (3.10)

Усі отримані результати зручно подати у вигляді результуючої матриці (табл. 3.1).

Таблиця 3.1 - Результуюча матриця для перевірки нуль-гіпотези

Джерело впливу	Кількість ступенів свободи	Сума квадратів відхилень SS	Середній квадрат відхилень S^2
Фактор xі		SSi
Фактор хj		SSj
Фактор xk		SSk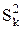
Похибка		SSε
Сума		SSΣ	-
Перевірка H0: F0,05; 3; 3

Дата добавления: 2015-08-17