Читайте также:
|
Параметрическое уравнение гиперболы в канонической системе координат имеет вид
где 
— гиперболический косинус, a 
гиперболический синус.
Действительно, подставляя выражения координат в уравнение (3.50), приходим к основному гиперболическому тождеству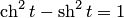 
.
Пример 3.21. Изобразить гиперболу 
в канонической системе координат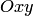 
. Найти полуоси, фокусное расстояние, эксцентриситет, фокальный параметр, уравнения асимптот и директрис.
Решение. Сравнивая заданное уравнение с каноническим, определяем полуоси: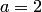 
— действительная полуось, 
— мнимая полуось гиперболы. Строим основной прямоугольник со сторонами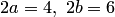 
с центром в начале координат (рис.3.44). Проводим асимптоты, продлевая диагонали основного прямоугольника. Строим гиперболу, учитывая ее симметричность относительно координатных осей. При необходимости определяем координаты некоторых точек гиперболы. Например, подставляя 
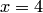в уравнение гиперболы, получаем
Следовательно, точки с координатам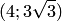и 
и 
принадлежат гиперболе. Вычисляем фокусное расстояние
эксцентриситет 
; фокальныи параметр 
. Составляем уравнения асимптот 
, то есть 
, и уравнения директрис: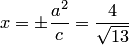 
.
Дата добавления: 2015-08-17; просмотров: 57 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Замечания 3.10. | | | Науково-технічний прогрес та економічне співробітництво. |