Фокальное свойство гиперболы

Точки и называются фокусами гиперболы, расстояние 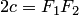между ними — фокусным расстоянием, середина 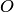отрезка — центром гиперболы, число — длиной действительной оси гиперболы (соответственно, — действительной полуосью гиперболы). Отрезк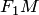и и 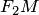, соединяющие произвольную точку гиперболы с ее фокусами, называются фокальными радиусами точки . Отрезок, соединяющий две точки гиперболы, называется хордой гиперболы.

Отношение , где 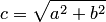, называется эксцентриситетом гиперболы. Из определения 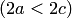следует, что .

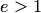Геометрическое определение гиперболы, выражающее ее фокальное свойство, эквивалентно ее аналитическому определению — линии, задаваемой каноническим уравнением гиперболы:

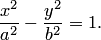
(3.50)

Действительно, введем прямоугольную систему координат (рис.3.40,б). Центр 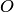гиперболы примем за начало системы координат; прямую, проходящую через фокусы (фокальную ось), примем за ось абсцисс (положительное направление на ней от точки к точке ); прямую, перпендикулярную оси абсцисс и проходящую через центр гиперболы, примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат 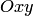оказалась правой).

Составим уравнение гиперболы, используя геометрическое определение, выражающее фокальное свойство. В выбранной системе координат определяем координаты фокусов 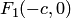и 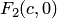. Для произвольной точки 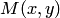, принадлежащей гиперболе, имеем:

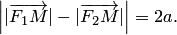
Записывая это уравнение в координатной форме, получаем:

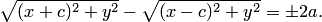
Выполняя преобразования, аналогичные преобразованиям, используемым при выводе уравнения эллипса (т.е. избавляясь от иррациональности), приходим к каноническому уравнению гиперболы:

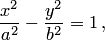
где 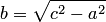, т.е. выбранная система координат является канонической.

Проводя рассуждения в обратном порядке, можно показать, что все точки, координаты которых удовлетворяют уравнению (3.50), и только они, принадлежат геометрическому месту точек, называемому гиперболой. Таким образом, аналитическое определение гиперболы эквивалентно его геометрическому определению.

Дата добавления: 2015-08-17