Замечания 3.10.

1. Прямые ограничивают на координатной плоскости основной прямоугольник, вне которого находится гипербола (рис.3.42,а).

2. Прямые , содержащие диагонали основного прямоугольника, называются асимптотами гиперболы (рис.3.42,а).

Для равносторонней гиперболы, описываемой уравнением (т.е. при 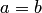), основной прямоугольник является квадратом, диагонали которого перпендикулярны. Поэтому асимптоты равносторонней гиперболы также перпендикулярны, и их можно взять в качестве координатных осей прямоугольной системы координат (рис.3.42,б). В этой системе координат уравнение гиперболы имеет вид (гипербола совпадает с графиком элементарной функции, выражающей обратно-пропорциональную зависимость).

В самом деле, повернем каноническую систему координат на угол 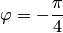(рис.3.42,б). При этом координаты точки в старой и новой системах координат связаны равенствами

Подставляя эти выражения в уравнение равносторонней гиперболы и приводя подобные члены, получаем

3. Координатные оси (канонической системы координат) являются осями симметрии гиперболы (называются главными осями гиперболы), а ее центр — центром симметрии.

Действительно, если точка 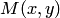принадлежит гиперболе . то и точки и , симметричные точке относительно координатных осей, также принадлежат той же гиперболе.

Ось симметрии, на которой располагаются фокусы гиперболы, является фокальной осью.

4. Из уравнения гиперболы в полярных координатах (см. рис.3.41,б) выясняется геометрический смысл фокального параметра — это половина длины хорды гиперболы, проходящей через ее фокус перпендикулярно фокальной оси ( при ).

5. Эксцентриситет характеризует форму гиперболы. Чем больше , тем шире ветви гиперболы, а чем ближе к единице, тем ветви гиперболы уже (рис.3.43,а).

Действительно, величина угла между асимптотами гиперболы, содержащего ее ветвь, определяется отношением сторон основного прямоугольника: . Учитывая, что и , получаем

Чем больше , тем больше угол . Для равносторонней гиперболы имеем и . Для угол тупой, а для угол острый (рис.3.43,а).

6. Две гиперболы, определяемые в одной и той же системе координат уравнениями и 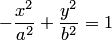называются сопряженными друг с другом. Сопряженные гиперболы имеют одни и те же асимптоты (рис.3.43,б). Уравнение сопряженной гиперболы 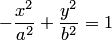приводится к каноническому при помощи переименования координатных осей (3.38).

7. Уравнение 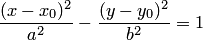определяет гиперболу с центром в точке 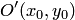, оси которой параллельны координатным осям (рис.3.43,в). Это уравнение сводится к каноническому при помощи параллельного переноса (3.36). Уравнение определяет сопряженную гиперболу с центром в точке .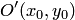

Дата добавления: 2015-08-17