Читайте также:
|
Директрисами эллипса называются две прямые, проходящие параллельно оси ординат канонической системы координат на одинаковом расстоянии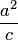 
от нее. При 
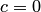, когда эллипс является окружностью, директрис нет (можно считать, что директрисы бесконечно удалены).
Эллипс с эксцентриситетом 
можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки 
(фокуса) к расстоянию до заданной прямой 
(директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету 
(директориальное свойство эллипса). Здесь и — один из фокусов эллипса и одна из его директрис, расположенные по одну сторону от оси ординат канонической системы координат, т.е. 
или 
.
В самом деле, например, для фокуса 
и директрисы 
(рис.3.37,6) условие 
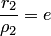можно записать в координатной форме:
Избавляясь от иррациональности и заменяя 
, приходим к каноническому уравнению эллипса (3.49). Аналогичные рассуждения можно провести для фокуса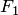 
и директрисы 
.
Дата добавления: 2015-08-17; просмотров: 150 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Фокальное свойство эллипса | | | Уравнение эллипса в полярной системе координат |