Замечания 3.9

1. Прямые ограничивают на координатной плоскости основной прямоугольник, внутри которого находится эллипс (см. рис.3.37,а).

2. Эллипс можно определить, как геометрическое место точек, получаемое в результате сжатия окружности к ее диаметру.

Действительно, пусть в прямоугольной системе координат уравнение окружности имеет вид . При сжатии к оси абсцисс с коэффициентом координаты произвольной точки , принадлежащей окружности, изменяются по закону

Подставляя в уравнение окружности и , получаем уравнение для координат образа 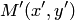точки :

поскольку 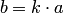. Это каноническое уравнение эллипса.

3. Координатные оси (канонической системы координат) являются осями симметрии эллипса (называются главными осями эллипса), а его центр — центром симметрии.

Действительно, если точка принадлежит эллипсу 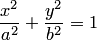. то и точк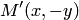и и , симметричные точке относительно координатных осей, также принадлежат тому же эллипсу.

4. Из уравнения эллипса в полярной системе координат (см. рис.3.37,в), выясняется геометрический смысл фокального параметра — это половина длины хорды эллипса, проходящей через его фокус перпендикулярно фокальной оси ( при ).

5. Эксцентриситет характеризует форму эллипса, а именно отличие эллипса от окружности. Чем больше , тем эллипс более вытянут, а чем ближе к нулю, тем ближе эллипс к окружности (рис.3.38,а). Действительно, учитывая, что и , получаем

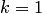где — коэффициент сжатия эллипса, . Следовательно, . Чем больше сжат эллипс по сравнению с окружностью, тем меньше коэффициент сжатия и больше эксцентриситет. Для окружности и .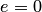

6. Уравнение 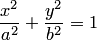при определяет эллипс, фокусы которого расположены на оси (рис.3.38,6). Это уравнение сводится к каноническому при помощи переименования координатных осей (3.38).

7. Уравнение определяет эллипс с центром в точке , оси которого параллельны координатным осям (рис.3.38,в). Это уравнение сводится к каноническому при помощи параллельного переноса (3.36).

При уравнение описывает окружность радиуса с центром в точке .

Дата добавления: 2015-08-17