Читайте также:
|
Уравнение эллипса в полярной системе координат 
(рис.3.37,в и 3.37(2)) имеет вид
где 
фокальный параметр эллипса.
В самом деле, выберем в качестве полюса полярной системы координат левый фокус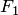 
эллипса, а в качестве полярной оси — луч 
(рис.3.37,в). Тогда для произвольной точки 
, согласно геометрическому определению (фокальному свойству) эллипса, имеем 
. Выражаем расстояние между точками и 
(см. пункт 2 замечаний 2.8):
Следовательно, в координатной форме уравнение эллипса 
имеет вид
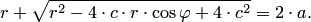
Уединяем радикал, возводим обе части уравнения в квадрат, делим на 4 и приводим подобные члены:
Выражаем полярный радиус 
и делаем замену 
:
что и требовалось доказать.
Дата добавления: 2015-08-17; просмотров: 133 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Директориальное свойство эллипса | | | Геометрический смысл коэффициентов в уравнении эллипса |