Читайте также:
|
Любой процесс распространения волны в пространстве описывается одним и тем же дифференциальным уравнением – волновым уравнением:
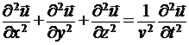
Используя оператор Лапласа, волновое уравнение можно записать в виде:
.
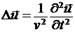Решением волнового уравнения всегда будет вол -новая функция
.
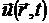Все результаты, полученные для монохроматической гармонической волны, будут справедливыми и для волн произвольной формы (сумма решений уравнения также является его решением). Поэтому далее будут исследоваться только монохроматические гармонические волны.
Коэффициент, который стоит при производной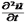 
в волновом уравнении, обязательно будет обратным квадратом скорости v волны. Это скорость перемещения волнового фронта и волновых поверхностей, т.е. точек, имеющих одинаковую фазу колебаний. Поэтому скорость v называют фазовой скоростью волны.
Используя оператор Лапласа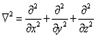 
, волновое уравнение можно записать в виде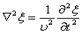 
Дата добавления: 2015-08-17; просмотров: 89 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Электромагнитные волны в средах с частотной дисперсией | | | Распространение радиоволн в земных условиях |