Интерференция и дифракция электромагнитных волн.

Интерференция – это явление сложения двух или нескольких волн, приходящих в точку приема из нескольких источников.

Дифракция – явление огибания эл.магн. волнами препятствия. Если электромагнитная волна определенного вида, например плоская или сферическая, падает на объект, отличающийся электродинамическими свойствами от окружающей среды, то имеет место дифракция волны на этом объекте.

Уравнению Гельмгольца 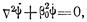где - коэффициент фазы волнового процесса при заданной частоте источника.

Любое решение уравнения Гельмгольца, обладающее свойством волны, уходящей на бесконечность, должно при 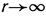удовлетворять предельному условию вида: Эту формулу называют условием излучения или условием Зоммерфельда.

13 Дифракция Френеля и Фраунгофера Дифракция Фраунгофера — случай дифракции, при котором дифракционная картина наблюдается на значительном расстоянии от отверстия или преграды. Если точка наблюдения Р отстоит от излучающего раскрыва на расстоянии, исчисляемом многими длинами волн, то ,и поэтому .При анализе антенных систем обычно приходится находить поле на расстоянии , значительно превышающем размеры раскрыва . При этом угол можно считать одинаковым для всех точек раскрыва, а расстояние , равным расстоянию от точки наблюдения до центра раскрыва. Величину , входящую в аргумент экспоненциальной функции, на основании сделанных предположений можно приближенно представить следующим образом: 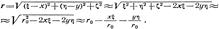Случай, когда оказывается справедливой эта формула, принято называть дифракцией Фраунгофера.

Дифракции Френеля, или дифракции в ближней зоне. Дифракция Френеля — дифракционная картина, которая наблюдается на небольшом расстоянии от препятствия, по условиям, когда основной вклад в интерференционную картину дают границы экрана.

Максимальная геометрическая разность хода 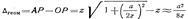соответствует фазовому сдвигу между колебаниями .Рис.1.Характер распределения в ближней зоне апертурной антенны. 1-лучевая трубка; 2 - сферическая волна. Дифракция Фраунгофера имеет место в том случае, если точка наблюдения Р столь удалена от излучающей системы, что (последняя цифра во многом условна и принята для конкретности оценок). Говорят, что при этом точка наблюдения находится в дальней зоне апертурной антенны. Поле в дальней зоне имеет вид неоднородной сферической волны.

Если приблизить точку наблюдения к излучающей апертуре, то максимальный фазовый сдвиг между элементарными колебаниями становится больше 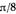.При этом точка наблюдения располагается в ближней зоне антенны. Условной границей между ближней и дальней зонами служит плоскость с координатой 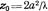.Анализ показывает, что для ближней зоны характерна локализация энергии электромагнитного поля в пределах «лучевой трубки» (рис.1), поперечник которой сравним с размерами апертуры. Чтобы вычислить дифракционное поле в ближней зоне, используем выражение для расстояния между точками источника и наблюдения, учитывающее квадратичные члены: .Принято говорить, что волновая картина, рассматриваемая в данном приближении, соответствует дифракции Френеля.

14 Электромагнитные волны в сверхпроводниках. Согласно модельным представлениям немецких физиков Ф. и Г. Лондонов, вещество в сверхпроводящем состоянии содержит носители заряда двух типов: нормальные носители, которые подчиняются обычным законам классической электродинамики, и сверхпроводящие носители, способные перемещаться в кристаллической решетке вещества без какого-либо сопротивления. Соответственно вектор плотности полного тока J в каждой точке сверхпроводника представляется суммой двух составляющих: , где индексы относятся к нормальной и сверхпроводящей компонентам соответственно. - лондоновская длина.

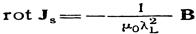- уравнение Лондонов. Согласно этому уравнению, плотность сверхпроводящего тока связана не с электрическим, а с магнитным полем.

15 Угол Брюстера.Полное внутреннее отражение. При падении плоских электромагнитных волн на границу раздела двух сред при определенных условиях коэффициент отражения может обращаться в нуль. Угол падения, при котором падающая волна полностью, без отражения, проникает из одной среды в другую, называется углом Брюстера и обозначается как φ_Б. φ_Б удовлетворяет одному из двух уравнений: (4,35) при перпендикулярной поляризации либо (4,36) при параллельной поляризации. Здесь под ψ_Б подразумевается угол преломления, соответствующий углу падения φ_Б. Легко видеть, что уравнения (4.35) и (4.36) взаимно противоречат друг другу, т. е. явление полного преломления можно наблюдать либо при перпендикулярной, либо при параллельной поляризации. Рассмотрим наиболее часто встречающийся случай, когда обе граничащие среды являются немагнитными (µ₁=µ₂=l), в то время как оптическая плотность второй среды больше, чем первой (ε₂>ε₁). Из данных предположений, во-первых, следует что Z_с1>Z_c2. Во-вторых, в силу закона Снелля φ>ψ, т. е. cos φ<cos ψ.

Обращаясь к формулам (4.35) и (4.36), видим, что первое из этих уравнений в рамках сделанных предположений принципиально не может иметь решений. Таким образом, угол Брюстера при падении плоской электромагнитной волны на немагнитный диэлектрик может существовать лишь при параллельной поляризации.

Сравнение графиков, зависимостей коэффициентов отражения для волн обеих поляризаций, представленных на рис. 4.8, иллюстрирует понятие угла Брюстера.Явление полного преломления может иметь полезные технические приложения. Так, пластинка из диэлектрика, установленная под углом Брюстера по отношению к направлению распространения падающей волны, не создает отражений. В то же время эта пластинка, может играть роль важного конструктивного элемента, обеспечивая, например, вакуумное уплотнение какого-либо прибора. Полное внутреннее отражение — внутреннее отражение, при условии, что угол падения превосходит некоторый критический угол. При этом падающая волна отражается полностью, и значение коэффициента отражения превосходит его самые большие значения для полированных поверхностей. Коэффициент отражения при полном внутреннем отражении не зависит от длины волны.В оптике это явление наблюдается для широкого спектра электромагнитного излучения, включая рентгеновский диапазон.В геометрической оптике явление объясняется в рамках закона Снелла. Учитывая, что угол преломления не может превышать 90°, получаем, что при угле падения, синус которого больше отношения меньшего показателя преломления к большему показателю, электромагнитная волна должна полностью отражаться в первую среду. В соответствии с волновой теорией явления, электромагнитная волна всё же проникает во вторую среду — там распространяется так называемая «неоднородная волна», которая экспоненциально затухает и энергию с собой не уносит. Характерная глубина проникновения неоднородной волны во вторую среду порядка длины волны.

Нарушенное полное внутреннее отражение — явление нарушения полного внутреннего отражения из-за поглощения отражающей средой части излучения. Широко применяется в лабораторной практике и оптической промышленности.

16 Замедление электромагнитных волн диэлектрической пластины. Рассматриваются электромагнитные процессы в системе, состоящей из диэлектрической пластины толщиной а, обладающей относительной диэлектрической проницаемостью ε, которая расположена на подложке из идеального проводника (рис. 11.4). Для простоты будем полагать, что диэлектрик немагнитный (µ_а = µ_а) и без потерь (σ = 0). Будет показано, что подобная пластина может играть роль волновода замедленных волн. Цель дальнейшего математического рассмотрения состоит в нахождении структуры электромагнитного поля замедленной волны, а также в определении коэффициента замедления системы. Будем решать задачу, рассматривая отдельно пространство, представляющее вакуум (область 1) и пространство внутри пластины (область 2); соответствующие индексы будут поставлены при составляющих электромагнитного поля. Сделаем три существенных предположения:

1) рассматриваемая волна является замедленной, поэтому длина волны в волноводе удовлетворяет неравенству λ_в<λ_о, которое, будучи записанным относительно продольного волнового числа h, приобретает вид: h>γ₀;

2) система неограниченно протяженна вдоль координат z и у, указанных на рис. 11.4; 3) изучаемое поле представляет собой волну, распространяющуюся вдоль координаты z, причем магнитный вектор имеет единственную составляющую, направленную по координате у. С учетом предыдущего условия это означает, что силовые линии магнитного поля имеют вид бесконечных нитей, вытянутых над пластиной. Обратимся к рассмотрению первой области. Для составляющей Ĥ_y1 имеем здесь уравнение Гельмгольца: 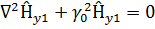(11.3) Решение этого уравнения будем искать в виде бегущей волны с неизвестными пока амплитудой и фазовой постоянной: (11.4) Подставляя (11.4) в (11.3) и учитывая, что по условию д/ду = 0 а также сокращая полученное выражение на общий экспоненциальный множитель, запишем обыкновенное дифференциальное уравнение (11.5) где , являющееся аналогом поперечного волнового числа в теории полых металлических волноводов, служит весьма важной характеристикой рассматриваемой системы. Отметим, что для замедленных волн число р всегда вещественно, поскольку h >γ_о. Общее решение уравнения (11.5) имеет вид (11.6)

где А, В — произвольные постоянные. Из физических соображений ясно, что В=0, т. К. поле не может неограниченно возрастать при удалении от направляющей системы.

Дата добавления: 2015-08-17