Сезонные фиктивные переменные

Рассмотрим методику моделирования сезонных колебаний с помощью фиктивных переменных. Как мы выяснили анализируемый ряд квартальной динамики представлен в виде аддитивной модели содержащей трендовую, сезонную и случайную компоненты. Тенденция описывается линейным трендом. Для описания сезонных колебаний используем фиктивные переменные. Тогда общий вид модели может быть записан следующим об­разом:

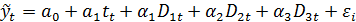
где

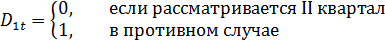
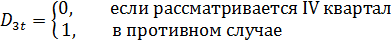
Заметим, что число кварталов равно четырем, а следователь­но, число фиктивных переменных должно быть равно трем. В нашем примере в качестве базы выбран I квартал. Если значе­ния y существенно различаются по кварталам (сезонам), то в уравнении коэффициенты при фиктивных переменных окажутся статистически значимыми. Тогда ожидаемое значение y по кварталам определяется следующими соотношениями:

Для I квартала:

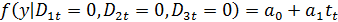
Для II квартала:

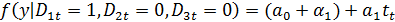
Для III квартала:

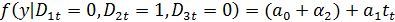
Для IV квартала:

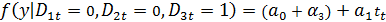
Легко видеть, что в приведенной модели рассматриваются такие ситуации, при которых квартальные различия отражаются лишь в различии свободных членов моделей. Если же различия затрагивают и изменения коэффициента пропорциональности, то этот факт может быть отражен в следующей модели:

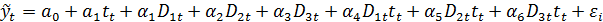
Выбор правильной формы модели регрессии является в данной ситуации достаточно серьезной проблемой, так как вполне вероятны ошибки спецификации. Наиболее рациональ­ной практической стратегией выбора модели является следую­щая схема.

Вначале рассматривается модель общая модель. Определяется ста­тистическая значимость коэффициентов. Если дифференциаль­ные угловые коэффициенты оказываются статистически незначимыми, то переходят к первой модели. Если в этой модели дифференциальные свободные члены оказываются статистиче­ски незначимыми, то делают вывод, что квартальные (сезонные) изменения несущественны для рассматриваемой зависимости.

Дата добавления: 2015-08-20