Регрессия с одной количественной и двумя качественными переменными

Рассмотрим модель одной количественной с двумя качествен­ными переменными.

Пример: y - заработная плата сотрудников фирмы, x - стаж работы, D₁ - наличие высшего образования, D₂ - пол со­трудника:

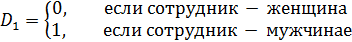
Таким образом, получим следующую модель:

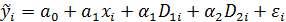
Из этой модели выводятся следующие регрессионные зави­симости.

Средняя заработная плата женщины без высшего образо­вания:

Средняя заработная плата женщины с высшим образова­нием:

Средняя заработная плата мужчины без высшего образо­вания:

Средняя заработная плата мужчины с высшим образова­нием:

Очевидно, что все регрессии отличаются лишь свободными членами. Дальнейшее определение статистической значимости коэффициентов a₁ и a₂ позволяет убедиться, влияют ли образо­вание и пол сотрудника на его заработную плату.

Естественно, что предложенные выше схемы могут быть распространены на ситуации с произвольным числом количест­венных и качественных факторов. При этом не следует забывать, что если качественный фактор имеет k альтернативных состояний, то для его описания используется (k - 1) фиктивных переменных.

Сравнение двух регрессий (тест Г.Чоу)

В реальной экономики могут возникнуть ситуации, когда изменение качественного фактора может привести к изменению, как свободного члена уравнения, так и наклона прямой регрессии.

Иногда выборка наблюдений состоит из двух или более подвыборок, и труд­но установить, следует ли оценивать одну объединенную регрессию или отдельные регрессии для каждой подвыборки.

Например, одна выборка пар значений переменных объемом T₁ получена при одних условиях, а другая, объемом T₂ при несколько измененных условиях.

t

t

Необходимо выяснить можно ли объединить две выборки в одну и рассматривать единую модель регрессии или прибегнуть к построению так называемой кусочно-линейной регрессии. Четкий ответ на данный вопрос дает тест (критерий) Г.Чоу (Chow Gregory).

В соответствии с предложенной Г.Чоу методикой первоначально определяем остаточную сумму квадратов по кусочно-линейной модели используя следующую формулу:

S^к-л_ост = S¹_ост + S²_ост

где: S^к-л_ост - остаточная сумма квадратов по кусочно-линейной модели;

Sⁱ_ост - остаточная сумма квадратов по i -му уравнению.

Соответствующее ей число степеней свободы составит:

(T₁-m₁)+(T₂-m₂) = T - m₁ - m₂

где: T – число наблюдений во всей совокупности;

m_i – число параметров в i -ом уравнении.

Тогда сокращение остаточной дисперсии при переходе от единого уравнения тренда к кусочно-линейной модели можно определить следующим образом:

DS_ост = S³_ост - S^к-л_ост

Число степеней свободы, соответствующее DS_ост будет равно:

T - m₃ - (T - m₁ - m₂) = m₁ + m₂ - m₃

В общем, виде расчетную таблицу для теста Г.Чоу можно представить в следующем виде.

Таблица 3- Условные обозначения для алгоритма теста Чоу

Периоды	Число наблюдений в совокупности	Остаточная сумма квадратов	Число параметров в уравнении	Число степеней свободы остаточной дисперсии
Первое уравнение	T1	S^1ост	m1	T1-m1
Второе уравнение	T2	S^2ост	m2	T2-m2
Объединенное уравнение	T	S^3ост	m3	T - m3 = =(T1+T2)-m3

Далее определим фактическое значение F -критерия Фишера по следующей формуле:

Далее находим F_табл с уровнем значимости a и числом степеней свободы (m₁+m₂-m₃) и (T-m₁-m₂).

Если F_факт>F_табл, то гипотеза об адекватности линейного тренда построенного на основе всей совокупности отвергается. Поэтому прогнозирование тенденции рассматриваемого ряда следует осуществлять с помощью кусочно-линейной модели.

Необходимо отметить, что использование указанной F -статистики (теста Чоу) осуществляется достаточно просто. Однако оно менее ин­формативно, нежели общий анализ сложной регрессии с фик­тивными переменными, осуществляемый на базе t -статистик (с учетом вклада каждой фиктивной переменной), коэффициента детерминации и статистики Дарбина-Уотсона. Однако тест Чоу вполне достаточен, если требуется установить, что зависимости в подвыборках различаются.

Дата добавления: 2015-08-20