Два временных тренда

Когда представлены два временных тренда, то фиктивная переменная должна быть выбрана для каждого из них. Эта задача может иметь два уровня сложности в зависимости от того, известно ли, какому тренду принадлежат данные, или же это не из­вестно.

1. Когда известно, какие точки принадлежат каким трендам. Пусть, например, есть два временных тренда, причем оба линейные. Тогда мы можем выделить в этой ситуации еще два подкласса:

- когда об абсциссе точки пересечения двух линий можно предположить, что она соответствует определенному значению, в котором есть одно или несколько наблюдений;

- когда абсцисса точки пересечения этих двух линий не известна.

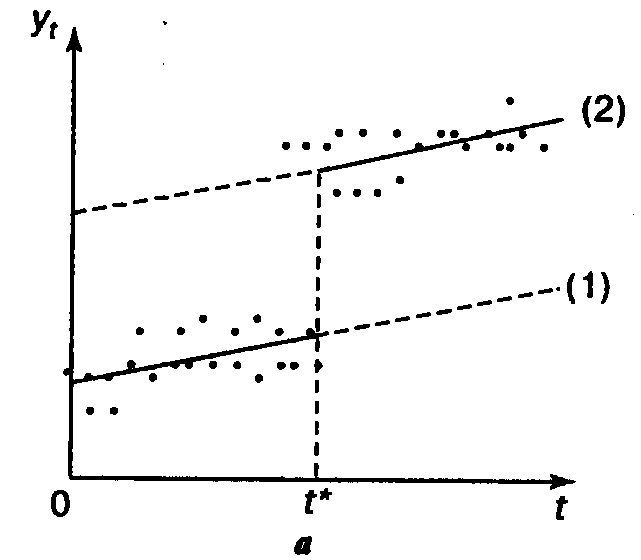
В качестве иллюстрации первого случая рассмотрим следующий пример. Известно, что первые пять точек лежат (если пренебречь случайной ошибкой) на первой прямой, а последние пять точек (опять же если пренебречь случайной ошиб­кой) - на второй. Значит, пятая точка в этом случае оказывается общей для обеих прямых.

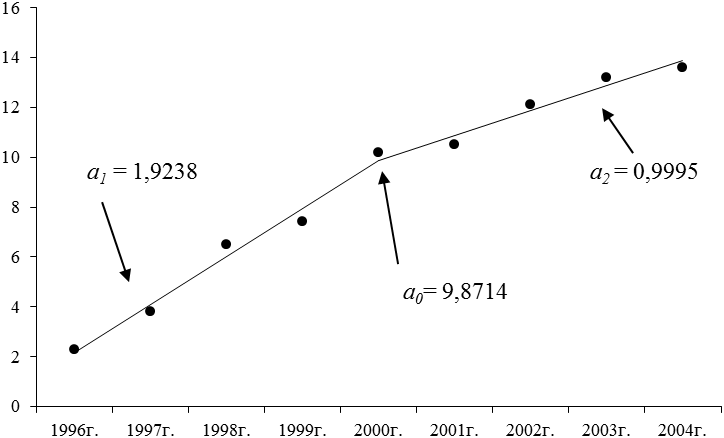
Рисунок 1 - Использование фиктивных переменных. Две линии, абсцисса точки пересечения известна

Мы можем ввести две фиктивные перемен­ные t₁ и t₂ для этих двух прямых следующим образом. Положим обе фиктивные переменные равными нулю в известной точке пересече­ния, а именно в точке пятого наблюдения, из которой t₁ для первой прямой пойдет назад, а t₂ для второй прямой - вперед, причем каждая переменная будет обращаться в нуль там, где действует другая. Получаем следующую таблицу с данными:

Таблица 1 - Фиктивные переменные для примера с двумя прямыми, абсцисса точки, пересечения которых известна

Дата	yt	t1	t2	Альтернативное представление
t1	t2
1996г.	2,3	-4
1997г.	3,8	-3
1998г.	6,5	-2
1999г.	7,4	-1
2000г.	10,2
2001г.	10,5
2002г.	12,1
2003г.	13,2
2004г.	13,6

Модель в данном случае имеет вид:

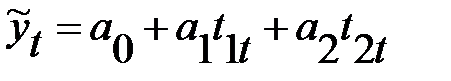
Полученные оценки имеют следующую интерпритацию:

а₀ - значение y в точке пересечения, t₁ = t₂ = 0;

а₁ - угловой коэффициент прямой первого тренда;

а₂ - угловой коэффициент прямой второго тренда.

Предложенное представ­ление фиктивных переменных не единственно. Пример альтернативного представления пока­зан в таблице 1, где (t новая) = (t₁ старая)+5. Это представле­ние даст точно такие же оценки угловых коэффициентов, что и преды­дущее, но зато постоянный член a₀, соответствующий значению y, когда t₁ = t₂ = 0, стал бы теперь свободным членом первого урав­нения.

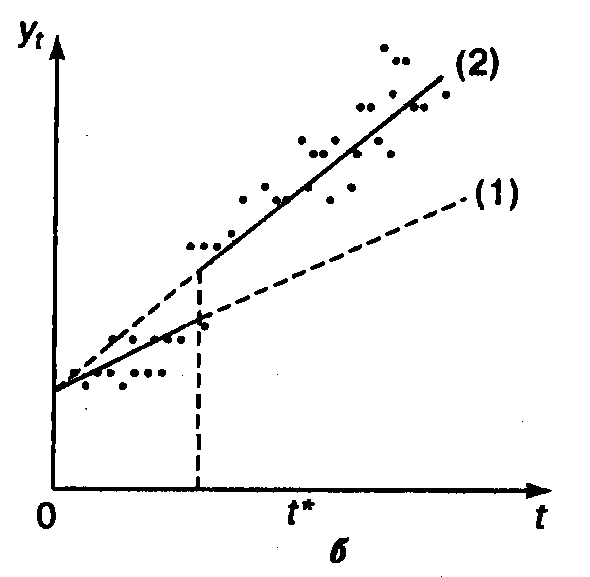
Рассмотрим пример относящийся ко второму ва­рианту. Здесь из­вестно, что первые че­тыре точки лежат (если пренебречь случайной ошибкой) на первой пря­мой, а последние пять (снова без учета случай­ной ошибки) - на вто­рой.

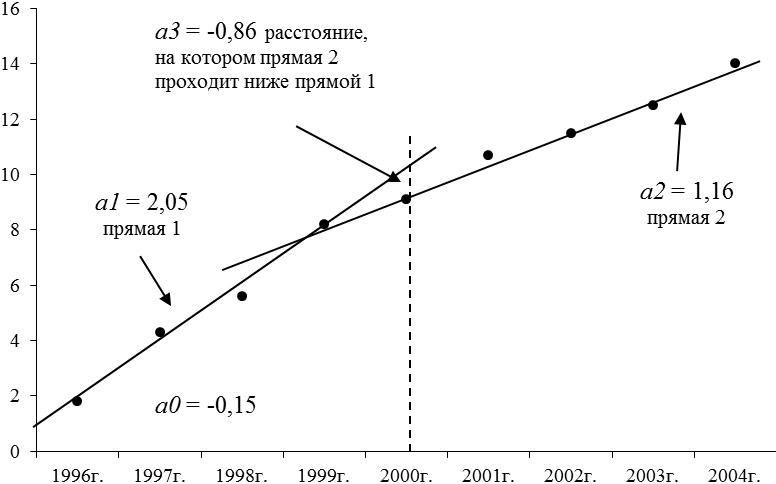
Рисунок 2 - Использование фиктивных перемен­ных. Две линии, абсцисса точки пересечения не известна

Однако точка их пересечения не известна. Чтобы обнаружить эту неизвестную точку, по­надобится третья фик­тивная переменная t₃. Ее естественно поло­жить равной нулю для всех точек первой прямой и соответственно единице для точек второй прямой, чтобы отразить скачок (положи­тельный или отрицательный) от первой прямой ко второй. Фиктив­ные переменные t₁ и t₂ выбираются точно так же, как это сделано в предыдущем примере.

Таблица 2 - Фиктивные переменные для примера с двумя прямыми, точка пересечения которых не известна

Дата	yt	t1	t2	t3
1996г.	1,8
1997г.	4,3
1998г.	5,6
1999г.	8,2
2000г.	9,1
2001г.	10,7
2002г.	11,5
2003г.	12,5
2004г.	14,0

В итоге имеем следующую модель:

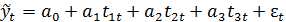
Параметр а₃ представляет собой шаг изменения, приводящий к эф­фекту наблюдения в пятой точке. Фактически это вертикальное рас­стояние, на котором в этой точке вторая прямая проходит выше пер­вой. (Если вторая прямая лежит ниже первой, то коэффициент а₃ будет отрицательным.)

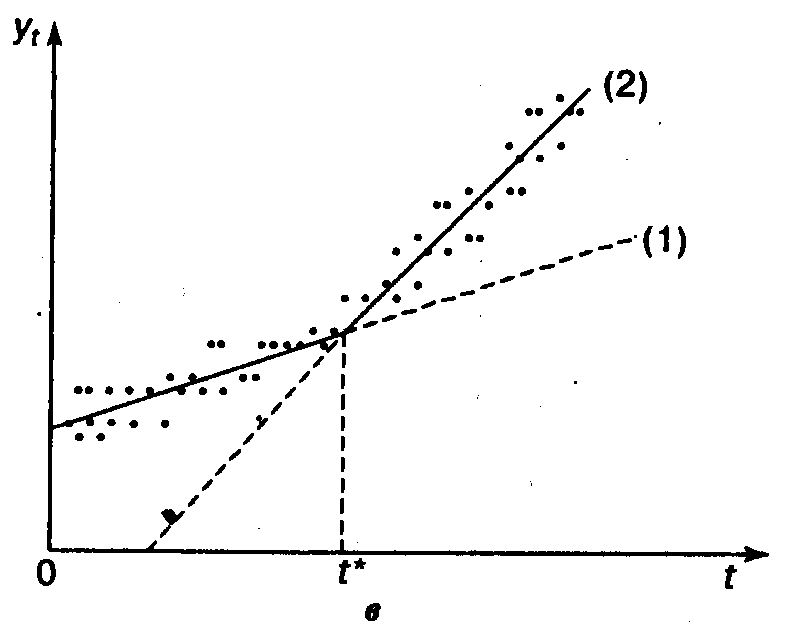
2. Когда не известно, какие точки относятся к какому тренду. В случае когда не известны точки пересечения прямых ре­шение следовало бы получать, просматривая все возможные варианты разбиения точек между двумя прямыми, оценивая в каждом таком разбиении параметры линейным методом наименьших квадратов и вычисляя остаточные суммы квадратов. А затем можно выбрать та­кое разбиение вместе с набором оценок параметров, которое порож­дает наименьшее из всех значение остаточной суммы квадратов. (На практике обычно нет никакой необходимости просматривать каж­дое возможное разбиение точек, поскольку даже малые вычисления обычно показывают ту «танцплощадку», где и находится наилучшее разбиение. Только этот ограниченный набор разбиений и надо сосчи­тать.) С другой стороны, эту задачу можно представить как задачу нелинейного оценивания.

Дата добавления: 2015-08-20