Уравнение Payчадхури - Ньюмена - Пенроуза

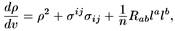
где п = 2 для нулевых геодезических,

п = 3 для времениподобных геодезических.

Здесь v является аффинным параметром вдоль конгруэнций геодезических с касательным вектором l ^а, который ортогонален к гиперповерхности. Величина ρ является средней скоростью сближения геодезических, в то время как σ измеряет напряжение. Слагаемое R_ab l ^a l ^bопределяет непосредственное гравитационное воздействие материи на сходимость геодезических.

Уравнение Эйнштейна

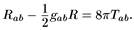
Слабое энергетическое условие

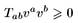
для любого времениподобного вектора v ^a.

Из уравнений Эйнштейна следует, что последнее слагаемое будет неотрицательным для любого нулевого вектора l ^а, если материя удовлетворяет так называемому слабому энергетическому условию. Оно утверждает, что плотность энергии T ₀₀ является неотрицательной в любом базисе. Слабому энергетическому условию удовлетворяет классический тензор энергии-импульса любого разумного вида материи, такого как скалярное или электромагнитное поле или жидкость с приемлемым уравнением состояния. Однако это условие может локально не выполняться для квантово-механического среднего

Классическая теория · 21

значения тензора энергии-импульса. Это будет существенно в моих второй и третьей лекциях (главы 3, 5).

Предположим, что слабое энергетическое условие справедливо, и что нулевые геодезические из точки p начинают снова сходиться, причем ρ имеет положительное значение ρ ₀· Тогда из уравнений Ньюмена-Пенроуза следует, что сближение ρ может стать бесконечным в точке q внутри промежутка аффинного параметра размером 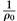, если нулевая геодезическая может быть так далеко продолжена.

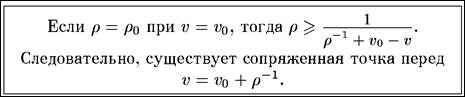
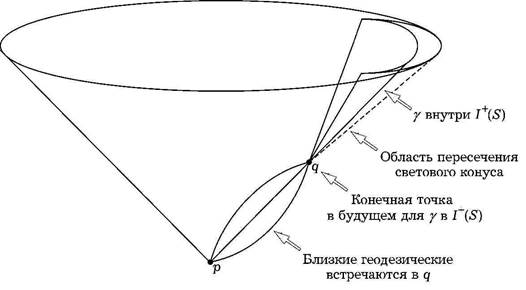
Бесконечно близкие нулевые геодезические из p будут пересекаться в q. Это означает, что точка q будет сопряжена с p вдоль соединяющей их нулевой геодезической γ. Для точек на γ кроме точки q будет существовать такая вариация γ, которая дает времениподобную кривую из р. Такая геодезическая γ не может лежать на границе будущего точки p за сопряженной точкой q. Таким образом, γ будет иметь конечную точку в будущем как генератор границы будущего точки p (см. рис. 1.9).

Сильное энергетическое условие

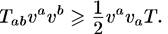
Ситуация с времениподобными геодезическими аналогична, за исключением того, что сильное энергетическое условие, необходимое для того, чтобы величина R_abl ^a l ^bбыла неотрицательной для любого времениподобного вектора l ^а, как следует из самого названия, является более сильным. Оно остается, однако, физически приемлемым в классической теории, по крайней мере в смысле средних значений. Если выполняется

22 • Глава 1 — Стивен Хокинг

сильное энергетическое условие, и времениподобные геодезические, выходящие из р, снова начинают сближаться, будет существовать точка q, сопряженная точке р.

Рис. 1.9. Точка q является сопряженной к р вдоль нулевых геодезических, так что нулевая Геодезическая γ, которая соединяет р с q, будет покидать границу будущего точки р в точке q.

Общее энергетическое условие:

1.Выполняется сильное энергетическое условие.

2. Каждая времениподобная или нулевая геодезическая содержит точку, где

Наконец, существует общее энергетическое условие. Оно утверждает, во-первых, что справедливо сильное энергетическое условие. Во-вторых, каждая времениподобная или нулевая геодезическая включает точку, где отлична от нуля кривизна, специально связанная со свойствами геодезической. Общее энергетическое условие не удовлетворяется для некоторых

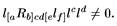
Классическая теория • 23

точных решений. Но эти примеры являются довольно специальными. Можно ожидать, что оно выполняется для решений, которые являются «общими» в подходящем смысле. Если общее энергетическое условие выполняется, то каждая геодезическая будет включать область гравитационного фокусирования. Отсюда вытекает, что если геодезические можно продолжить достаточно далеко в каждом направлении, то должны существовать пары сопряженных точек.

Естественно представлять себе пространственно-временную сингулярность как область, в которой кривизна становится неограниченно большой. Однако, принимая это как определение, мы сталкиваемся с проблемой, так как можно просто вырезать сингулярные точки и сказать, что остающееся многообразие и было всем пространством-временем. Поэтому лучше определить пространство-время как максимальное многообразие, на котором метрика является достаточно гладкой. Тогда можно заметить появление сингулярностей по существованию неполных геодезических, которые не могут быть продолжены на бесконечные значения аффинного параметра.

Дата добавления: 2015-08-20