Глава 3. Квантовые черные дыры. Стивен Хокинг

В своей второй лекции я хочу поговорить о квантовой теории черных дыр. Мне кажется, что она ведет к новому уровню непредсказуемости в физике сверх обычной неопределенности, связанной с квантовой механикой. Это происходит потому, что черные дыры имеют внутреннюю энтропию, что приводит к потере информации из нашей области Вселенной. Должен сказать, что эти утверждения являются спорными: многие люди, работающие в квантовой гравитации, включая почти всех, кто пришел туда из физики частиц, будут инстинктивно отвергать идею о том, что информация о квантовом состоянии системы может быть утеряна. Однако все эти ученые достигли весьма скромных успехов, пытаясь показать, как можно извлечь информацию из черной дыры. Я уверен, что в конце концов они будут вынуждены принять мое утверждение о том, что информация теряется, как раньше вынуждены были согласиться с тем, что черные дыры излучают, хотя это находится в полном противоречии со всеми их убеждениями.

Начну с напоминания классической теории черных дыр. В прошлой лекции мы видели, что гравитация всегда действует как притягивающая сила, по крайне мере, в нормальной ситуации. Если бы гравитация иногда действовала как притягивающая, а иногда — как отталкивающая сила, как в электродинамике, мы не замечали бы ее вообще, потому что гравитационная сила в 10⁴⁰ (ДА НУ НА ХУЙЮ, СТЕПЕНЬ ЕБНУТАЯ) раз слабее электромагнитных сил. Только благодаря тому, что гравитационные силы между частицами двух макроскопических тел, подобных нашим телам и Земле, складываются, они приводят к силе, величину которой мы можем почувствовать.

Квантовые черные дыры · 49

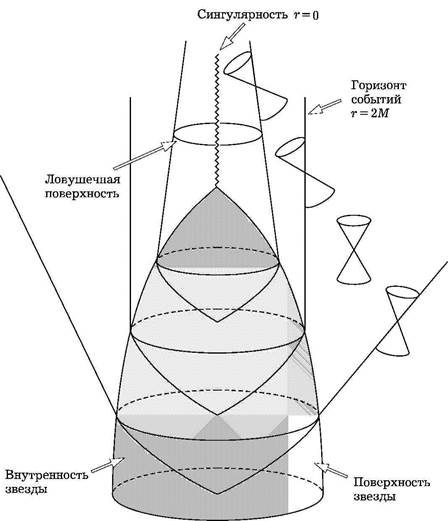
Рис. 3.1. Пространственно-временная картина коллапса звезды с образованием черной дыры. Показан горизонт событий и замкнутая ловушечная поверхность

То, что гравитация всегда является притягивающей силой, означает, что она старается собрать вместе всю материю во Вселенной, чтобы образовать объекты, подобные звездам и галактикам. В течение некоторого времени эти объекты удерживаются от дальнейшего сжатия за счет теплового давления, в случае звезд, или вращения и внутреннего движения, в случае галактик. Однако в конце концов теплота и момент импульса рассеиваются, и объект начинает сжиматься. Если масса объекта меньше 1,5 масс Солнца, сжатие может быть

50 · Глава 3 — Стивен Хокинг

остановлено за счет давления вырожденного газа электронов или нейтронов. Тогда образуется белый карлик или нейтронная звезда, соответственно. Однако, если масса больше указанного предела, то не существует ничего, что могло бы остановить неудержимое сжатие. После того, как тело сожмется до определенного критического размера, гравитационное поле на его поверхности становится настолько сильным, что световые конусы оказываются наклоненными внутрь этой поверхности, как на рис. 3.1. Я предпочел бы нарисовать четырехмерную картину, однако в результате урезания бюджета Кембриджский университет может позволить себе только двумерные экраны. Поэтому в вертикальном направлении я буду показывать время, а два из трех пространственных направлений буду изображать с помощью перспективы. Вы можете видеть, что даже выходящие световые лучи наклонены друг к другу и поэтому они не расходятся, а сближаются. Это означает, что существует замкнутая ловушечная поверхность, наличие которой является одной из возможных формулировок третьего условия теоремы Хокинга-Пенроуза.

Если верна гипотеза космической цензуры, то она предсказывает, что ловушечная поверхность и сингулярность не могут быть видны с большого расстояния. Тогда должна существовать такая область пространства-времени, из которой невозможно уйти на бесконечность. Эту область называют черной дырой. Ее граница называется горизонтом событий. Она является нулевой поверхностью, образованной теми световыми лучами, которые как раз не смогли уйти на бесконечность. Как мы видели в последней лекции, площадь поперечного сечения горизонта событий не может уменьшаться, по крайней мере в классической теории. Это, а также расчеты сферического коллапса по теории возмущений наводят на мысль, что черные дыры находятся в стационарном состоянии. Теорема «об отсутствии волос» у черной дыры, доказанная в совместной работе Израэли, Картера, Робинсона и моей, показывает, что только стационарные черные дыры в отсутствии материальных полей могут соответствовать решениям Керра. Они характеризуются двумя параметрами, массой Μ и моментом импульса J. Теорема об отсутствии волос была рас-

Квантовые черные дыры · 51

пространена Робинсоном на случай наличия электромагнитного поля. Это добавляет третий параметр Q, электрический заряд. Теорема об отсутствии волос не доказана для случая полей Янга-Миллса, но, похоже, единственной разницей будет добавление одного или нескольких целых чисел, нумерующих дискретное семейство нестабильных решений. Можно показать, что в случае независящих от времени черных дыр, описываемых уравнениями Эйнштейна-Янга-Миллса, не существует других непрерывных степеней свободы.

Дата добавления: 2015-08-20