Метрика Шварцшильда

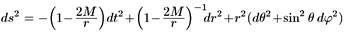
Эта метрика соответствует гравитационному полю, которое создает невращающаяся черная дыра. В обычных координатах r и t эта метрика обладает кажущейся особенностью при шварцшильдовском радиусе r = 2М. Однако эта особенность является лишь следствием плохого выбора координат. Можно выбрать другие координаты, в которых метрика в этой точке будет регулярной.

Диаграмма Картера-Пенроуза имеет вид ромба, со срезанными верхом и низом (рис. 3.4). Она делится на четыре области двумя нулевыми поверхностями, на которых r = 2М. Область справа, отмеченная на диаграмме как является

асимптотически плоским пространством, в котором, как мы полагаем, мы и живем. Она имеет нулевые бесконечности и в прошлом и в будущем, подобно плоскому пространству-времени. С левой стороны диаграммы существует другая асимптотически плоская область , которая, по-видимому, соответствует другой вселенной, связанной с нашей только гор-

Квантовые черные дыры · 57

ловиной. Однако, как мы увидим, она связана с нашей областью с помощью мнимого времени. Нулевая поверхность, идущая снизу слева вверх направо, является границей области, из которой можно уйти на правую бесконечность. Поэтому она является горизонтом событий будущего, причем эпитет «будущий» добавлен для того, чтобы отличать его от горизонта событий прошлого, идущего снизу справа вверх налево.

Рис. 3.4. Диаграмма Картера —Пенроуза для вечно существующей шварцшильдовской черной дыры

Вернемся теперь к метрике Шварцшильда в первоначальных координатах r и t. Если положить t = iτ, получается положительно определенная метрика. Я буду называть такие метрики евклидовыми, хотя они могут соответствовать искривленному пространству. В такой евклидово-шварцшильдовской метрике по-прежнему существует кажущаяся сингулярность при r = 2М. Однако можно определить новую радиальную координату х, равную 4M (l — 2 Mr ^-1) ^1/2.

Дата добавления: 2015-08-20