Слабая космическая цензура.

Если слабая космическая цензура выполняется, то сингулярности, которые, как предсказано, появляются при гравитационном коллапсе, не могут быть видимыми из . Это означает, что должна существовать область пространства-времени, которая не находится в прошлом для 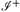. Эту область называют черной дырой, потому что ни свет, ни что-либо еще не может оторваться от нее и уйти на бесконечность. Границу черной дыры называют горизонтом событий. Поскольку она так же является границей прошлого для 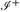, горизонт событий может быть получен с помощью отрезков нулевых геодезических, которые могут иметь конечную точку в прошлом, но не могут иметь каких-либо конечных точек в будущем. Из этого следует, что если слабое энергетическое условие выполнено, то генераторы горизонта не могут сближаться, т. к. если бы

32 · Глава 1 — Стивен Хокинг

Рис. 1.16. Когда мы бросаем материю в черную дыру или разрешаем двум черным дырам сливаться, общая площадь горизонта событий никогда не убывает

это происходило, они пересекались бы друг с другом на конечных расстояниях. Отсюда следует, что площадь поперечного сечения горизонта событий не может уменьшаться с течением времени, а в общем случае только увеличивается. Более того, если две черные дыры сталкиваются и сливаются вместе, площадь поверхности конечной черной дыры будет больше, чем сумма площадей поверхностей первоначальных черных дыр (рис. 1.16). Это очень похоже на поведение энтропии в соответствии со вторым законом термодинамики. Энтропия тоже никогда не может уменьшаться, и энтропия полной системы больше, чем сумма энтропий составляющих ее частей.

Дата добавления: 2015-08-20