Космическая цензура.

Природа питает отвращение к голой сингулярности.

Однако, как я покажу в следующей лекции, в квантовой теории существует некоторая непредсказуемость. Это связано с тем, что гравитационное поле имеет внутреннюю энтропию, что является не только следствием крупнозернистой структу-

30 · Глава 1 — Стивен Хокинг

ры. Гравитационная энтропия, а также тот факт, что время имеет начало и может иметь конец, являются темами моих следующих лекций, потому что это есть как раз то, что существенно отличает гравитацию от других физических полей.

Рис. 1.15. Коллапсирующая звезда, конформно вложенная в многообразие с границей

То, что гравитация имеет характеристику, которая ведет себя подобно энтропии, сначала был отмечен в чисто классической теории. Это зависит от предложенного Пенроузом принципа космической цензуры. Сам принцип не доказан, но считается, что он справедлив при достаточно общих начальных данных и уравнениях состояния. Я буду использовать слабую форму космической цензуры. Сделаем приближение, считая, что область в окрестности коллапсирующей звезды является асимптотически плоской. Тогда, как показал Пенроуз, можно конформно вложить пространственно-временное многооб-

Классическая теория · 31

разие М в многообразие с границей Μ (рис. 1.15). Граница дМ будет нулевой поверхностью и будет состоять из двух компонент, нулевой бесконечности в будущем и в прошлом, называемых 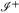и . Я буду говорить, что слабая космическая цензура выполнена, если удовлетворяются два условия. Во-первых, предполагается, что нулевые геодезические генераторы в являются полными в определенной конформной метрике. Это приводит к тому, что наблюдатели, далекие от коллапса, живут до старости и на них не влияет разрыв сингулярности, исходящей от коллапсирующей звезды. Во-вторых, предполагается, что прошлое для является глобально гиперболическим. Это означает, что не существует голой сингулярности, которую можно увидеть с большого расстояния. Пенроуз использовал более сильную форму космической цензуры, которая предполагает, что пространство-время в целом является глобально гиперболическим (ПОЛНОСТЬЮ СОГЛАСЕН). Но слабая форма будет вполне достаточной для моих целей.

Дата добавления: 2015-08-20