Читайте также:
|
Рынок состоит из двух рисковых активов A 1, A 2 и одного безрискового A 0. Параметры рынка
Безрисковая доходность m0, вектор ожидаемых доходностей рисковых активов - m = 
(m1 ¹ m2) и матрица ковариации рисковых активов C =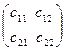 
.
где веса x 1 и x 2 любые вещественные числа. Полный вектор m ожидаемых доходностей
m = 
Полная матрица ковариаций С:
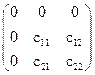
Портфель и его характеристики. Портфель задается полным вектором весов х:
x 0 + x 1 + x 2 = 1
где
x = 
- рисковая часть портфеля.
Ожидаемая доходность портфеля есть (учитывая, что х0 =1- x 1 - x 2)
E[ x ] = (m, x) = m0x0 + m1x1 + m2x2 = m0 +(m1-m0)x1+(m2-m0)x2 = m0+(m0, x)
где
m0 = 
Риск (вариация) есть
V[ x ] = (Сx, x) = (Сx, x) = c11 (x1)2 + c22 (x2)2 + 2c12x1x2,
Полезность портфеля
U[ x ] = E[ x ] – (q/2)V[ x ] = (m0, x) - (q/2)(С x, x) =
= m0 +(m1-m0)x1+(m2-m0)x2 -(q/2)(c11∙x12 + c22 ∙ x2 2 +2c12 x1x2)
Таким образом, характеристики портфеля зависят только от рисковой части портфеля, что существенно упрощает задачи оптимизации портфелей, поскольку эти задачи становятся задачами безусловной оптимизации.
Дата добавления: 2015-08-20; просмотров: 58 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Из первого уравнения получаем | | | Задача 5. |