
Читайте также:
|
Вивчаючи те чи інше явище, ми часто змушені мати справу з величинами, які пов’язані між собою так, що зміна деяких з них приводить до зміни інших. Такий взаємозв’язок у математиці виражається за допомогою поняття функції. Наприклад площа круга радіуса 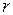 виражається формулою:
виражається формулою: 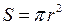 . Змінюючи радіус
. Змінюючи радіус 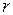 , ми відповідним чином будемо змінювати і площу, отже ми можемо сказати, що площа круга
, ми відповідним чином будемо змінювати і площу, отже ми можемо сказати, що площа круга  є функцією його радіуса
є функцією його радіуса 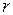 . Згідно з законом всесвітнього тяжіння, сила, з якою тіла масами
. Згідно з законом всесвітнього тяжіння, сила, з якою тіла масами 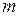 та
та  взаємодіють між собою, виражається формулою:
взаємодіють між собою, виражається формулою:
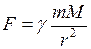 , де
, де 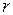 – відстань між центрами тіл,
– відстань між центрами тіл,  – універсальна гравітаційна стала. Залишаючи
– універсальна гравітаційна стала. Залишаючи 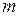 та
та  незмінними, ми можемо змінювати відстань
незмінними, ми можемо змінювати відстань 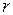 , і тоді відповідним чином буде змінюватися сила
, і тоді відповідним чином буде змінюватися сила 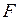 , тобто тут ми можемо сказати, що
, тобто тут ми можемо сказати, що 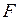 є функцією
є функцією 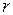 .
.
Дамо тепер означення функції.
Означення. Якщо кожному числу  з деякої числової множини
з деякої числової множини 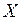 за певним законом поставлено у відповідність одне і тільки одне число
за певним законом поставлено у відповідність одне і тільки одне число 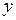 з числової множини
з числової множини 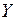 , то кажуть, що на множині
, то кажуть, що на множині 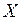 задано функцію
задано функцію  .
.
Змінна  називається незалежною змінною, або аргументом. Змінна
називається незалежною змінною, або аргументом. Змінна 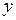 називається залежною змінною, або саме функцією. Під символом
називається залежною змінною, або саме функцією. Під символом 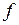 ми розуміємо як раз той самий закон, за яким встановлюється відповідність, тобто ті операції, які треба виконати над аргументом
ми розуміємо як раз той самий закон, за яким встановлюється відповідність, тобто ті операції, які треба виконати над аргументом  , щоб дістати відповідне значення функції
, щоб дістати відповідне значення функції 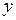 .
.
Множина 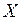 називається областю визначення функції і позначається
називається областю визначення функції і позначається  . Множина
. Множина 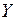 називається множиною значень функції і позначається
називається множиною значень функції і позначається  . Наприклад, для функції
. Наприклад, для функції 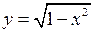 областю визначення є відрізок
областю визначення є відрізок 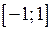 , а множиною значень відрізок
, а множиною значень відрізок 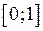 . Декількам різним значенням аргумента
. Декількам різним значенням аргумента  може відповідати одне й те ж значення функції
може відповідати одне й те ж значення функції 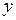 , зокрема у наведеному прикладі різним значенням аргумента
, зокрема у наведеному прикладі різним значенням аргумента 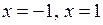 відповідає одне й те ж значення функції
відповідає одне й те ж значення функції 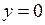 . Але наведене означення функції забороняє ситуацію, коли одному й тому ж значенню аргумента відповідає декілька різних значення функції. Хоча в інших розділах математичного аналізу, наприклад теорії функцій комплексної змінної, розглядаються і такі (так звані багатозначні) функції.
. Але наведене означення функції забороняє ситуацію, коли одному й тому ж значенню аргумента відповідає декілька різних значення функції. Хоча в інших розділах математичного аналізу, наприклад теорії функцій комплексної змінної, розглядаються і такі (так звані багатозначні) функції.
Розглянуті у попередній лекції послідовності теж можна розглядати як функції, область визначення яких є множина 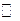 :
:
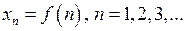
Функцію можна задавати різними способами.
1. Аналітичний спосіб. Це спосіб задання функції за допомогою формули (аналітичного виразу):
 , або
, або  .
.
Наприклад, формула  – це аналітичний спосіб задання функції, яка кожному дійсному значенню аргумента
– це аналітичний спосіб задання функції, яка кожному дійсному значенню аргумента  ставить у відповідність значення
ставить у відповідність значення  .
.
Аналітичний спосіб має як свої переваги, так і свої недоліки. До переваг відносяться компактність, зручність при проведенні теоретичних досліджень та ін. До недоліків – відсутність наглядності, необхідність проводити обчислення для знаходження значень функції та ін.
2. Табличний спосіб. Це спосіб задання функції за допомогою таблиці, до якої занесено значення функції при деяких обраних значеннях аргумента:

| 
| 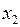
| … | 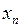
|
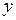
| 
| 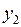
| … | 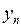
|
Тут 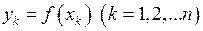 .
.
Наприклад, для функції  ця таблиця може мати такий вид:
ця таблиця може мати такий вид:

| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | |
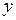
| 0,01 | 0,04 | 0,09 | 0,16 | 0,25 |
Цей спосіб часто використовують при проведенні експериментів, коли задають певну сукупність 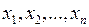 значень аргумента і дослідним шляхом знаходять відповідні значення функції
значень аргумента і дослідним шляхом знаходять відповідні значення функції  . Крім того, табличний спосіб широко застосовується при розв’язанні математичних задач за допомогою комп’ютерів, коли вихідну інформацію комп’ютер видає у вигляді числових масивів (таблиць). Зі школи вам знайомі відомі «Чотиризначні математичні таблиці» В.М.Брадіса. Дуже часто доводиться користуватися таблицями і при розв’язанні географічних задач (наприклад, у картографії, топографії).
. Крім того, табличний спосіб широко застосовується при розв’язанні математичних задач за допомогою комп’ютерів, коли вихідну інформацію комп’ютер видає у вигляді числових масивів (таблиць). Зі школи вам знайомі відомі «Чотиризначні математичні таблиці» В.М.Брадіса. Дуже часто доводиться користуватися таблицями і при розв’язанні географічних задач (наприклад, у картографії, топографії).
Цей спосіб також має переваги та недоліки. До переваг відноситься те, що не треба обчислювати значення функції (вони вже є у таблиці) До недоліків громіздкість (таблиці займають багато місця), відсутність наглядності, а також те, що принципово неможливо без додаткової інформації знайти значення функції для тих значень аргумента, які не входять до таблиці (а іноді це треба робити). Правда, якщо є деяка додаткова інформація про властивості функції, то можна наближено знайти ці значення за допомогою так званої інтерполяції.
3. Графічний спосіб. Це спосіб задання функції за допомогою графіка, тобто множини точок на координатній площині, прямокутні координати  яких задовольняють рівність
яких задовольняють рівність  . Залежно від того, яку задано функцію, графік її може складатися з однієї суцільної лінії, кількох ліній, дискретної множини точок тощо. Наприклад, графік функції
. Залежно від того, яку задано функцію, графік її може складатися з однієї суцільної лінії, кількох ліній, дискретної множини точок тощо. Наприклад, графік функції  має вид (славнозвісна парабола):
має вид (славнозвісна парабола):
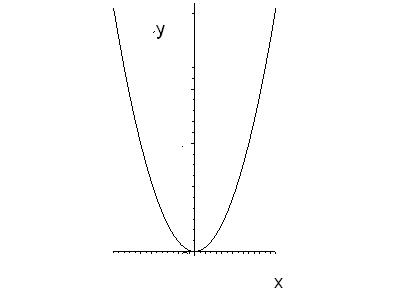 Рис. 14
Рис. 14
Графічним способом широко користуються при дослідженнях, пов’язаних з використанням таких засобів, як барограф (для запису змін атмосферного тиску), осцилограф (для запису змін електричного струму, чи напруги), електрокардіографа (для запису електричних явищ, пов’язаних з діяльностю серця), термографа (для запису температури повітря) тощо. Криві (відповідно барограма, осцилограма, електрокардіограма, термограма), які виписують ці прилади, задають певну функцію, властивості якої характеризують перебіг того, чи іншого процесу.
До переваг графічного способу відноситься, перш за все, наглядність (те, чого не мають аналітичний та табличний способи). Маючи графік, можна наглядно уявити собі характер процесу, який цим графіком описується. Разом з цим графічний спосіб має і недоліки: громіздкість, лише наближене уявлення про значення функції при конкретних значеннях аргумента.
4. Словесний спосіб. Існують функції, які складно, або взагалі неможливо задати формулою, а також неможливо побудувати графік. Деякі з таких функцій можна описати просто за допомогою слів. Класичним прикладом такої функції є так звана функція Діріхле*:
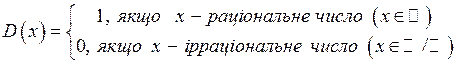
Графік цієї функції практично зобразити не можна, оскільки він складається з точок прямої  , які мають раціональні абсциси, і точок прямої
, які мають раціональні абсциси, і точок прямої 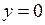 , які мають ірраціональні абсциси. Формулою задати, взагалі кажучи, можливо, але дуже складно. А таблиця значень цієї функції теж не може значно допомогти, оскільки буде містить лише два значення функції, до того ж неможливо задати скінченим десятковим дробом ірраціональне значення аргумента.
, які мають ірраціональні абсциси. Формулою задати, взагалі кажучи, можливо, але дуже складно. А таблиця значень цієї функції теж не може значно допомогти, оскільки буде містить лише два значення функції, до того ж неможливо задати скінченим десятковим дробом ірраціональне значення аргумента.
Ті функції, з якими ми у подальшому будемо мати справу, складаються з порівняно невеликого числа функцій, які називаються основними елементарними функціями. До них відносяться наступні функції.
1. Сталі функції, або константи.
Це функції виду 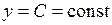 (тобто у кожній точці така функція приймає одне й те ж значення). Областю визначення
(тобто у кожній точці така функція приймає одне й те ж значення). Областю визначення  такої функції є проміжок
такої функції є проміжок 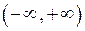 , а множиною значень
, а множиною значень  лише точка
лише точка  . Графіком такої функції є пряма лінія, яка паралельна осі абсцис і проходить через точку
. Графіком такої функції є пряма лінія, яка паралельна осі абсцис і проходить через точку  на осі ординат (рис. 15).
на осі ординат (рис. 15).
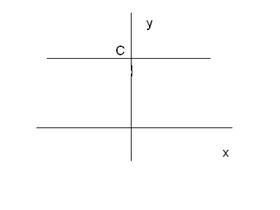
Рис. 15
2. Степеневі функції. Це функції виду  , де
, де 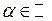 . Область визначення і множина значень такої функції залежить від
. Область визначення і множина значень такої функції залежить від  . Наведемо деякі приклади таких функцій та їх графіків.
. Наведемо деякі приклади таких функцій та їх графіків.
1) 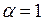 ;
;  .
.
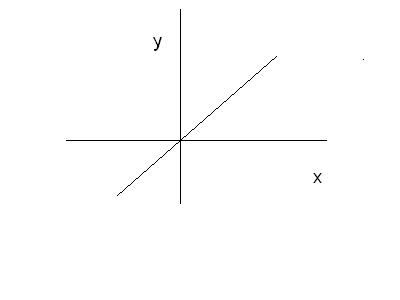
Рис. 16
2) 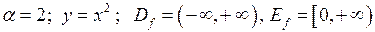 . Графік наведено на рис. 14.
. Графік наведено на рис. 14.
3)  . Графіком є так звана кубічна парабола:
. Графіком є так звана кубічна парабола:
 Рис. 17
Рис. 17
4) 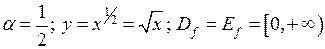 .
.

Рис. 18
5) 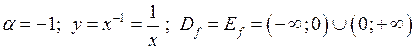 . Графік такої функції уявляє собою гіперболу (див. розділ «Аналітична геометрія на площині»):
. Графік такої функції уявляє собою гіперболу (див. розділ «Аналітична геометрія на площині»):
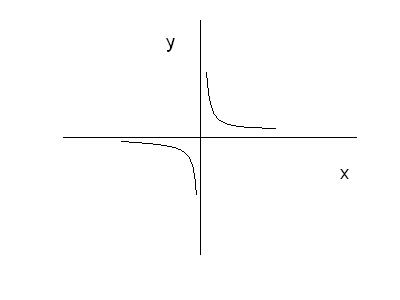
Рис. 19
6) 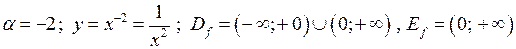 .
.
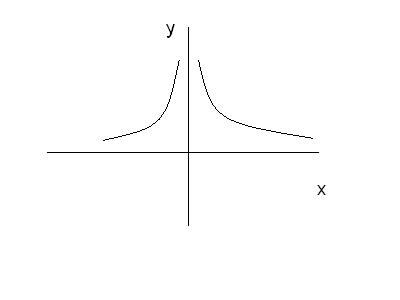
Рис. 20
3. Показникові функції:  . Характер графіка функції залежить від числа
. Характер графіка функції залежить від числа 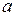 :
:
1) 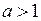 2)
2) 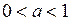

 Рис. 21 (а) Рис. 21 (б)
Рис. 21 (а) Рис. 21 (б)
Зокрема, до таких функцій належить славнозвісна експонента, про яку мова буде йти у наступних лекціях.
4. Логарифмічні функції: 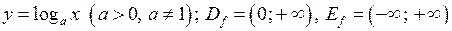 . Характер графіка також залежить від числа
. Характер графіка також залежить від числа 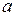 :
:
1) 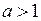 2)
2) 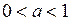
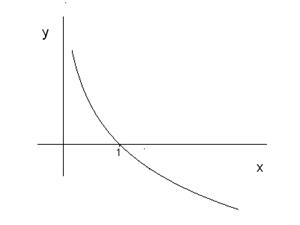

Рис. 22 (а) Рис. 22 (б)
5. Тригонометричні функції:
1)  .
.
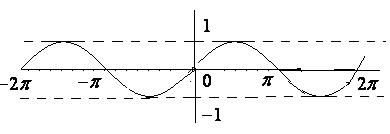
Рис. 23 (а)
2) 
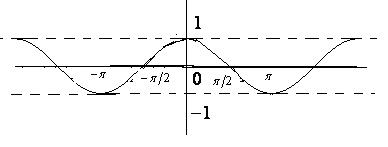
Рис. 23 (б)
3) 
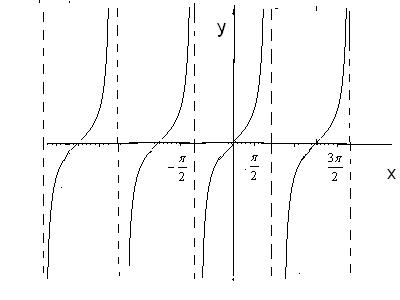
Рис. 24 (а)
4) 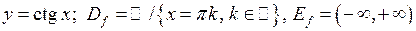
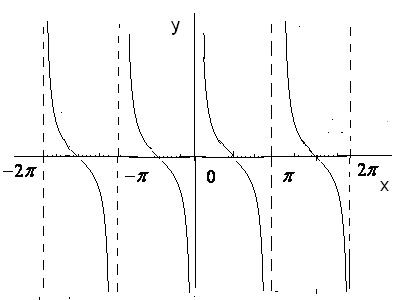
Рис. 24 (б)
6. Обернені тригонометричні функції.
1) 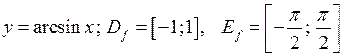
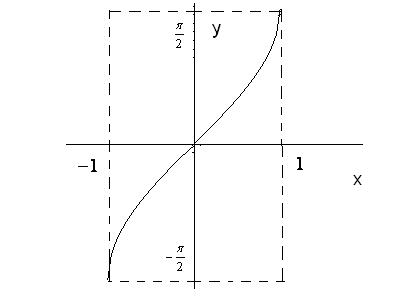 Рис. 25 (а)
Рис. 25 (а)
2) 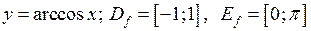
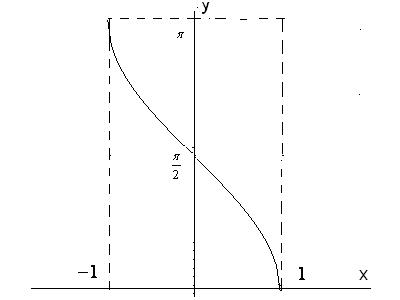 Рис. 25 (б)
Рис. 25 (б)
3)  .
.
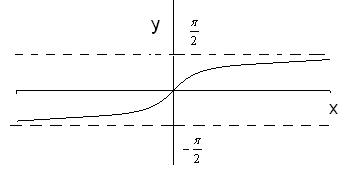 Рис. 26 (а)
Рис. 26 (а)
4) 
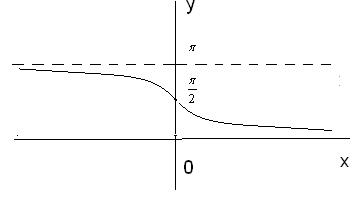
Рис. 26 (б)
* Діріхле Петер Густав Лежен (1805–1859) – німецький математик. Зробив значний внесок у розвиток теорії чисел та математичного аналізу.
Дата добавления: 2015-08-02; просмотров: 1176 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Числова послідовність та її границя. | | | Застосування судами законодавства, яке регулює поруку |