Література.

1. Дубовик В.П., Юрик І.І. Вища математика. К.: Вища школа, 1993.

2. Дубовик В.П., Юрик І.І. (ред.) Вища математика. Збірник задач. К.: АСК, 2005.

3. Кудрявцев В.А, Демидович Б.П. Краткий курс высшей математики. М.:Астрель, 2004.

4. Шипачёв В. С. Высшая математика. М.: Высшая школа, 1990.

5. Минорский В.П. Сборник задач по высшей математике. М.: Наука, 1987.

6. Самнер Г. Математика для географов. М.:Прогресс, 1981.

7. Игошин Н.И. Математические методы в физической географии. Одесса: Астропринт, 2005.

8. Диденко А.В., Щёголев С.А. Пределы последовательностей и функцій (основы теории и методы вычислений). Одесса: Астропринт, 1998.

Лекція 1. Деякі поняття теорії множин.

Під математичним аналізом (або просто аналізом) у математиці розуміється сукупність її розділів, присвячених дослідженню функції методами так званих нескінченно малих. Цей метод мав своє започаткування ще в стародавні часи (Євдокс, Архімед та ін.), але послідовна теорія була створена лише в XYII–XYIII ст. н.е. у працях І.Ньютона, Г.Лейбніца, а потім Л.Ейлера, К.Гауса, Ж.Лагранжа, О.Коші, К.Вейєрштрасса та ін.

Як і інші науки, математика ґрунтується на деяких поняттях, які неможливо визначити через інші поняття, і які являються початковими. Вважається, що ці поняття можна зрозуміти на інтуїтивному рівні. Одним з таких понять є поняття множини. Під множиною ми розуміємо сукупність деяких об’єктів, взагалі кажучи, довільної природи. Як правило, представляють інтерес сукупності таких об’єктів, які поєднуються якою-небудь спільною ознакою, чи властивістю. Наприклад, множина студентів у групі, множина наукових теорій, множина планет у Сонячній системі, множина країн, що входять до СОТ, множина чисел у проміжку (0;1) та ін.

Об’єкти, які складають множину, називаються елементами множини. Якщо цих елементів скінчена кількість, то множина називається скінченою, у протилежному випадку нескінченною. Наприклад, множина карт у гральній колоді скінчена, а множина трикутників, подібних даному – нескінченна.

Домовимось позначати множини великими буквами латинського алфавіту , а їх елементи відповідно малими: 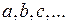. Якщо елемент 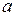належить множині 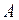, то пишемо: . Якщо не належить, то пишемо: .

Множина, яка не містить жодного елемента, називається порожньою і позначається символом . Наприклад порожньою множиною є множина від’ємних коренів рівняння .

Для запису множини використовуються фігурні дужки, елементи множини відокремлюються комами. Наприклад:

.

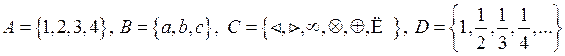Множина нескінченна. У більш детальних математичних курсах демонструється принципова різниця у властивостях скінчених та нескінченних множин.

Дві множини називаються рівними, якщо вони складаються з одних і тих же елементів. Наприклад, множина і – рівні (порядок слідкування елементів не відіграє ролі). Пишемо: .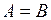

Множина називається підмножиною множини 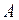, якщо кожен елемент множини являється елементом множини 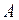. Пишемо: . Зокрема множина може співпадати з множиною 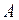. Тоді пишемо: 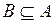. Наприклад, якщо , то , .

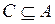Порожня множина є підмножиною будь якої множини. Дійсно, нехай 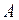– довільна множина. Якщо припустити, що не є її підмножиною, то у множині знайдеться принаймні один елемент, який не належить множині 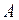. Але тоді вийшло б, що містить принаймні один елемент, що суперечить означенню порожньої множини.

Приклад. Задана множина 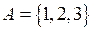. Записати всі підмножини цієї множини.

Маємо:

.

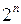Тобто всього 8 підмножин. Можна легко показати, що множина, яка містить елементів, має підмножин, враховуючи саму цю множину і порожню множину.

Визначимо деякі операції, які можна виконувати над множинами.

Множину , яка містить ті та тільки ті елементи, які належать хоча б одній з множин 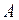і , називається об’єднанням множин 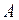і , і позначається: .

Множина , яка містить ті та тільки ті елементи, які належать водночас обом множинам 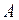і , називається перетином множин 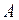і , і позначається: .

Приклад. Нехай . Тоді

.

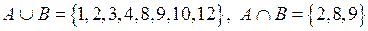Поняття об’єднання і перетину множин наглядно ілюструються геометрично (рис.1):

Рис. 1

Якщо множини 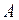і умовно зобразити кругами з різними штриховками на площині, то перетин множин 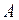і – це область, де присутні обидві штриховки (спільна частина кругів), а об’єднання цих множин – область, де є хоч би одна штриховка.

Різницею множин 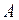і , назвемо всі елементи множини 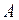, які не входять до множини . Позначається: . Тобто тоді і тільки тоді, коли . Наприклад, якщо , то . На рис.2 наведено геометричну ілюстрацію цього поняття:

Рис.2

Штриховкою показана множина .

Нехай задана довільна система множин 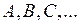Множину назвемо універсальною множиною для цієї системи, якщо кожна множина цієї системи являється підмножиною множини , тобто
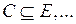(рис.3).

Рис.3

Доповненням множини 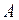до універсальної називається множина . Наприклад, якщо – множина натуральних чисел, 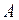– множина парних чисел, то – множина непарних чисел (враховуючи одиницю). Графічна ілюстрація показана на рис.4

Рис.4

Визначимо деякі властивості дій над множинами:

1) ,

2) ,

3) ,

4) ,

5) ,

6) ,

7) ,

8) ,

9) ,

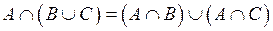10) ,

11) ,

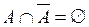12) ,

13) ,

14) .

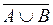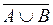Дві останні властивості називаються законами де Моргана. Аналоги цих законів є також в алгебрі висловлювань та теорії ймовірностей. Доведемо властивість 13). Щоб це зробити, треба показати, що будь який елемент, який належить множині , належить також і , і навпаки, будь який елемент, який належить , належить також і . Отже, нехай 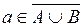. Тоді 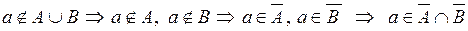. Навпаки, нехай . Тоді 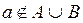. А звідси випливає, що 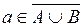, що й треба було довести.

Властивість 14) спробуйте довести самостійно.

У подальшому ми часто будемо використовувати слідуючи символи (так звані квантори):

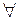– квантор загальності. Означає “для будь якого”, “для кожного”, “для всіх”. Походить від англійського слова Any – будь який (береться перша буква цього слова і перегортається).

– квантор існування. Означає “існує”, “знайдеться”, “можна вказати”. Походить від англійського слова Existence – існування.

Використання цих символів дозволяє значно скоротити запис багатьох формуліровок. Запишемо, наприклад, за допомогою кванторів таке твердження: “для будь якого додатного числа знайдеться інше додатне число 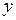, яке більше, ніж ”. Воно буде мати такий вигляд:

.

Лекція 2. Основні числові множини. Дійсні числа. Числова

Дата добавления: 2015-08-02