Вісь, проміжки на ній. Модуль дійсного числа.

У математиці виключно важливу роль відіграють числові множини, тобто такі, елементами яких являються числа. Розглянемо найбільш важливі з них:

1. Множина натуральних чисел .

Це числа, які ми використовуємо при рахуванні предметів. Множина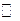

нескінченна, тобто .

Сума і добуток двох натуральних чисел також число натуральне. А ось різниця двох натуральних чисел не завжди є числом натуральним, наприклад .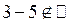

2. Множина цілих чисел . На множині 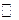вже можна здійснювати і операцію віднімання, тобто .

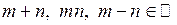Цілі числа мають низку дуже цікавих властивостей. Дослідженню цих властивостей присвячено такий розділ математики, як теорія чисел. Видатний німецький математик К.Ф. Гаус вважав теорію чисел царицею математики.

Частка від ділення двох цілих чисел не завжди є цілим числом, наприклад .

3. Множина раціональних чисел .

Раціональним ми називаємо число, яке можна зобразити у вигляді від-

ношення двох цілих чисел:

, де .

Сума, добуток, різниця і частка двох раціональних чисел є також число раціональне. Будь яке раціональне число можна зобразити у вигляді скінченого, або нескінченного періодичного десяткового дробу. Наприклад:

.

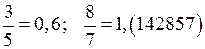Між будь якими двома раціональними числами завжди знайдеться принаймні ще одне (а отже нескінченна кількість) раціональних чисел. Дійсно, якщо , то число і задовольняє нерівність: .

Довгий час математики вважали, що раціональні числа вичерпують собою всі можливі числа. Деякі підстави у них для цього були: за допомогою раціональних чисел розв’язувалися практично всі задачі того часу. Представники філософської школи Піфагора вважали, що саме раціональне число лежить в основі світу. На підставі властивостей раціональних чисел ними, зокрема, була побудована теорія гармонії. Але потім виявилось, що існують задачі, розв’язання яких потребує виходу за межі множини раціональних чисел. Розглянемо таку задачу: знайти гіпотенузу прямокутного трикутника, обидва катети якого дорівнюють 1. Згідно з теоремою того ж Піфагора, легко знаходимо, що , отже у сучасному запису . Чи є це число раціональним? Припустимо, що це так, тоді (не обмежуючи загальності, ці числа можна вважати натуральними, а не тільки цілими, оскільки ) такі, що

.

Ми можемо також вважати, що дріб – нескоротний, оскільки, якщо це не так, то ми його скоротимо настільки, наскільки це можливо, і зробимо з нього нескоротний.

Оскільки 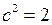, то 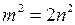, а це означає, що 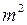– число парне. Тоді і 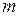– парне. Дійсно, якщо це не так, то , і тоді – непарне, що суперечить встановленому. Отже , і тоді , звідки 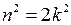, тобто 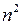– парне, а тоді, аналогічно попередньому, і – число парне. А якщо – парні, то дріб – скоротний, що суперечить припущенню.

Таким чином ми довели, що число не є раціональним. Такі числа називаються ірраціональними. До них відносяться, зокрема, також (доведіть самостійно), , славнозвісне число та інші. Будь яке ірраціональне число зображується у вигляді нескінченного і неперіодичного десяткового дробу. Наприклад, , .

4. Множина дійсних чисел .

Об’єднання множин раціональних та ірраціональних чисел складає

множину дійсних чисел. На цій множині визначені операції додавання, віднімання, множення, ділення (крім ділення на нуль), і результат цих операцій теж число дійсне. Не можна на множині добувати корінь парного степеня з від’ємного числа (ця операція виводить за межі множини дійсних чисел і приводить до так званих комплексних чисел, про які мова буде йти у наступних розділах курсу).

Дійсні числа мають зручну геометричну інтерпретацію. Введемо наступне поняття.

Числовою віссю називається пряма лінія, на якій обрано напрям, який умовно вважається додатним, початок відліку (точка 0) і одиниця ділення (рис. 5).

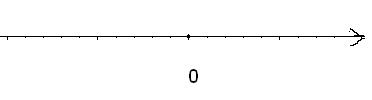
Рис. 5

Тоді будь якому дійсному числу відповідає одна і тільки одна точка числової осі, і навпаки, кожній точці числової осі відповідає одне і тільки одне дійсне число (рис. 6).

Рис. 6

Таким чином між множиною дійсних чисел і множиною точок числової осі встановлено взаємно однозначну відповідність. Тому ми часто замість терміну “дійсне число ” будемо вживати термін “точка ”.

Нехай 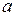і – дійсні числа, причому .

Відрізком (сегментом) числової осі називається множина точок осі, що задовольняє нерівність .

Інтервалом числової осі називається множина точок осі, що задовольняє нерівність .

Півсегментом (півінтервалом) чи числової осі називається множина точок осі, що задовольняє нерівність чи .

Суттєвою відмінністю відрізка від інтервалу є те, що точки відрізку належать, а інтервалу не належать. В півінтервалі одна з цих точок йому належить, а інша ні.

Інтервали та півінтервали, зокрема, можуть бути і нескінченними: .

Нехай – довільне дійсне число. Околом точки називається будь який інтервал 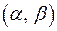, який містить точку , тобто .

Наприклад, інтервали є околами точки . Зауважимо, що точка , взагалі кажучи, не зобов’язана бути центром інтервалу 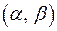(рис. 7).

Рис. 7

Задамо тепер дійсне число .

–околом точки називається інтервал .

Тепер вже точка є центром цього інтервалу. Число називають радіусом околу (рис. 8).

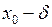
Рис. 8

Нехай задано дійсне число .

Модулем (абсолютною величиною) числа називають число 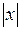, яке визначається за формулою:

Наприклад: .

З геометричної точки зору 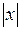дорівнює відстані від точки до початку координат (рис. 9).

Рис. 9

Сформулюємо найбільш важливі властивості модуля: виконано:

1) .

2) 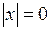тоді і тільки тоді, коли .

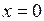3) .

4) .

5) .

6) .

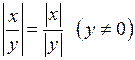7) .

8) .

Нехай – дві точки числової осі. Відстань між ними, очевидно, дорівнює (рис. 10).

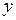
Рис. 10

Розглянемо –окіл точки і припустимо, що – довільна точка цього околу (рис. 11).

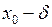
Рис. 11

Тоді очевидно, що . Справедливо і зворотне, тобто якщо виконано , то . Зокрема, якщо , де 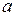– деяке додатне число, то і навпаки.

Виключимо з околу саму точку , тобто розглянемо множину . Тоді отримаємо так званий окіл з виколотою точкою . Для будь якого з цього околу виконано: .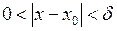

Лекція 3. Деякі задачі, які приводять до поняття границі.

Дата добавления: 2015-08-02