Потребителями

В конце предыдущего параграфа указывался метод определения средней цены мотивации с использованием функции распределения (4-4).

Поэтому представляется возможным дать определение средней арифметической мотивируемой потребителями цены на товар: средняя арифметическая цена на товар, мотивируемая мысленно 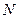потребителями, число которых достаточно велико, характеризуется как отношение суммы всех цен, мысленно мотивируемых потребителями 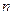, например, в единице объёма маркетингового пространства мотивации, к числу этих потребителей 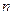в той же единице объёма.

Тогда число потребителей в единице объёма, мысленно назначаемые цены которые заключены в интервале значений цен от 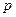до 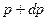, будет

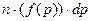. (4-26)

Поэтому сумма цен всех таких потребителей, если цены этих потребителей колеблются от 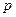до 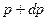в единице объёма составит

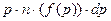. (4-27)

Но, чтобы найти сумму цен всех потребителей 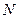, мысленно назначаемых товару теоретически любые цены, необходимо функцию (4-27), для которой долевое участие потребителей при мотивации цен в сумме равняется единице, проинтегрировать в диапазоне возможных назначаемых цен, то есть от нуля до бесконечности.

Вывод формулы для вычисления средней цены приводится ниже.

Формулу для средней мотивируемой всеми потребителями цены можно получить, следуя данному определению средней арифметической мотивируемой потребителями цены на товар (см. п. 4.3). Тогда число потребителей в единице объёма, мысленно назначаемые цены которых заключены в интервале значений цен от 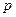до 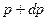, будет

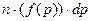. (4-28)

Поэтому сумма цен всех таких потребителей, если цены этих потребителей колеблются от 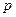до 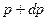в единице объёма составит

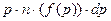. (4-29)

Поэтому сумма всех мотивированно назначаемых цен составит:

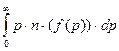, (4-30)

а средняя арифметическая цена, мотивированная всеми потребителями 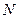, равна

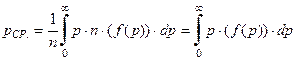. (4-31)

Подставив полученную функцию плотности распределения (4-4), получим:

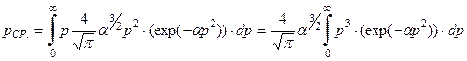, (4-32)

Приведение подинтегрального выражения к табличному виду для вычисления интеграла осуществим следующим образом:

,

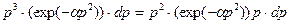но 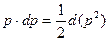, поэтому

,

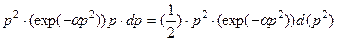что позволяет сделать замену переменной .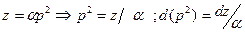

Тогда

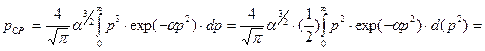
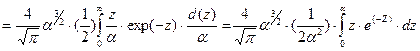. (4-33)

Интеграл 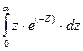можно определить «по частям» [306, 307] и будет равен:

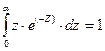. (4-34)

Тогда

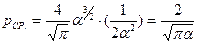, (4-35)

где параметр функции распределения 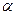полностью характеризуется проявлениями и особенностями кривой рис. 4.2., имеющей принципиально одну и ту же форму.

Поэтому средняя мотивируемая всеми потребителями цена определяется как 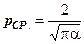. (4-36)

Наивероятнейшая цена - это цена в точке экстремума куполообразной кривой распределения (4-4). Исследование функций на экстремум широко известно и состоит в приравнивании нулю первой производной от функции плотности полученного распределения (4-4). Получение выражения для вычисления наивероятнейшей цены приведено ниже.

Формулу для определения наивероятнейшей цены можно получить путём исследования функции плотности (4-4) на экстремум. Исследование функций на экстремум широко известно и состоит в приравнивании нулю первой производной функции по интересуемому параметру. Поэтому:

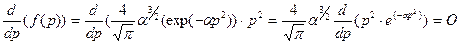, (4-37)

при этом 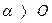, в связи с чем (4-37) равно нулю только при условии, что

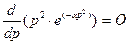(4-38)

Дифференцируя (4-38), получаем:

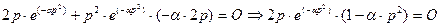, (4-39)

что позволяет выделить из произведения сомножители, равные нулю:

или 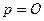(1), или 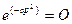(2), или 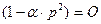(3);

решение 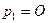(1) и решение 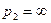(2) находятся в пределах границ допустимого диапазона значений мотивируемых цен, в связи с чем, эти цены не могут рассматриваться как наивероятнейшие цены. Поэтому решение следует искать в виде реализации условия (3):

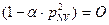(4-40)

Из (4-40) следует:

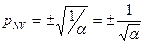. (4-41)

Учитывая, что цена, в том числе и наивероятнейшая, всегда больше нуля, из (4-41) выделяем положительное решение:

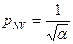(4-42)

Таким образом, наивероятнейшая цена, как и средняя цена мотивации в наибольшей степени зависит в простейшем случае только от формы кривой распределения, в свою очередь определяемой статистическими данными вероятностных оценок для цен, мотивируемых потребителями.

Представляет интерес определение отношения наивероятнейшей цены к средней цене. Тогда разделив (4-42) на (4-36), получим:

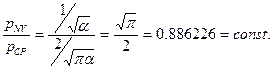(4-43)

Таким образом, отношение наивероятнейшей цены мотивации к средней цене мотивации в простейшем маркетинговом пространстве мотивационного поведения потребителей представима как величина постоянная и равная .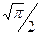

Дата добавления: 2015-08-10