Обработка данных и проверка статистической гипотезы на соответствие нормальному закону распределения полученных массивов данных.

Полученные массивы статистических данных, характеризующие параметр процесса вдоль одного координатного измерения за двадцатисекундный период, требует в статистическом плане определённые объёмы исследуемых выборочных совокупностей [243]. Поэтому для осуществления достоверной оценки предполагаемой гипотезы о нормальности распределения потребителей или ее отрицания, по таблице достаточно больших чисел [243, c.490] при доверительной вероятности 0,8 и ошибке 0,10 было определено количество экспериментальных серий 41 [243

Учитывая, однако, что существенное влияние на статистические колебания данных оказывают как длительность временных интервалов, так и общее число интервалов, на которые разбивается весь массив статистических данных в каждой серии, было организовано объединение статистических данных в каждой серии путём удлинения временных интервалов: 0,33 мин.; 0,66 мин.; 1,00 мин.; 1,33 мин., … М*0,33 мин., где М= 1, 2, 3, …. В таком случае по таблице достаточно больших чисел [243, c.490] число статистических данных в каждой серии при доверительной вероятности 0,92 и ошибке 0,10 определено минимальным числом 77. Фактически число статистических данных в основном определялось в пределах 90 – 200. Указанное объединение массивов данных, позволяющее организовывать другие массивы с более удлинёнными периодами временных интервалов, осуществлялось программно.

Листинг программы оценки стационарности общего потока потребителей на рынок и с рынка в соответствии с алгоритмом

10 DIM X(300), Y(300), Y1(300) 15 YminX(300) 20 FOR I = 1 TO 300 30 INPUT X(I) 40 IF X(I) = 0 THEN 60 50 NEXT I 60 N = I - 1 75 M = 1: N1 = N 78 PRINT “NASALO AZJOTA” 80 LNY = 0: X1 = 0: X2 = 0: YX = 0 81 X3 = 0: X =.2 + (M - 1) *.2 82 DX = X 83 FOR I = 1 TO N1 STEP M 84 Y(I) = X(I) 85 FOR J = 1 TO M - 1 88 Y(I) = Y(I) + X(I + J) 89 NEXT J: NEXT I 90 FOR I = 1 TO N1 STEP M 100 LNY = LNY + LOG(Y(I)) 110 X1 = X1 + X 111 X3 = X3 + X ^ 3 114 X2 = X2 + X ^ 2 120 YX = YX + LOG(Y(I)) * X 130 X = X + DX 140 NEXT I 150 ALFA = (X1 * LNY - N1 * YX) / (N1 * X3 - X1 * X2) 160 A = (1 / N1) * (LNY + ALFA * X2) 170 AYP = EXP(A) 180 X = DX 190 FOR I = 1 to N1 STEP M 200 Y1(I) = AYP * EXP(-ALFA * (X ^ 2)) 210 X = X + DX 220 NEXT I

230 X + DX 240 SY = 0: SY1 = 0 250 FOR I = 1 TO N1 STEP M 260 YminX(I) = Y(I) - Y1(I) 270 SY = SY + Y(I) 280 SY1 = SY1 + Y1(I) 290 NEXT I 300 SYSR = SY / N1: SY1SR = SY1 / N1 310 SyminX = 0: SS1 = 0: SS2 = 0 320 FOR I = 1 TO N1 STEP M 330 SyminX = SyminX + YminX(I) 340 SS1 = SS1 + (Y(I) - SYSR) ^ 2 350 SS2 = SS2 + (Y1(I) - SY1SR) ^ 2 360 NEXT I 370S1KV = SS1 / (N1 - 1) 375 S2KV = SS2 / (N1 - 1) 380 IF S1KV >= S2KV THEN 410 390 F = S2KV / S1KV 395 GOTO 415 410 F = S1KV / S2KV 415 YminXSR = SYminX / N1 420 SSYminX = 0 430 FOR I = 1 TO N1 STEP M 440 SSYminX = SSYminX + (YminXSR - YminX(I)) ^ 2 450 NEXT I 460 S = (SSYminX / (N1 - 1)) ^.5 470 T = YminXSR / (S / (N1 ^.5)) 480 PRINT “Prodolgenie scjota:sag M=”, M 481 PRINT “N1=”; N1; “F=”; F; “t=”; T 488 M = M + 1 489 N1 = INT(N / M) 490 IF N1 > 10 THEN 80 495 PRINT “Konez” 500 END

Полученные варианты массивов статистических данных в каждой серии аппроксимировались затем методом наименьших квадратов с использованием (наложением) функции плотности вероятностей для нормального закона распределения, ординаты которого позволили получить другой массив теоретических данных, сравнимый (согласно технике статистических вычислений [243, с. 304-365]) с соответствующим массивом данных, статистически собранных и обработанных программой компьютера (Рис. 3.1). Представленные два массива и позволяют осуществить оценку средних значений их разностей с применением t- статистики Стьюдента, поскольку данные, полученные наилучшим приближением к нормальному закону распределения весьма и весьма неоднозначны с точки зрения сходимости с исходными, полученными экспериментально статистическими данными.

Результаты расчётов, приведенные в табл. 3.1, убедительно доказывают статистическую совместимость исходных данных с предполагаемым нормальным законом распределения, что доказывает получение абсолютно для всех вариантов в каждой серии удовлетворяющего неравенства при уровне значимости для одностороннего критерия (Q) 0,01 и для двухстороннего критерия (2Q) 0,02 [243, с.350-355]:

, (3-1)

где

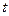- расчётное значение критерия Стьюдента для данного варианта образуемых данных статистической серии;

- табличное значение соответствующего критерия Стьюдента [243, c.538] для экспериментальной серии статистических данных.

Следует отметить, что, несмотря на достаточно удовлетворительную сходимость данных к нормальному закону распределения, варианты статистических серий весьма чувствительны к влиянию различных факторов как внешних, так и внутренних (статистических). К внешним факторам следует отнести влияние на стационарность разностного потока потребителей работы транспортных маршрутов (автобусы и трамваи). К внутренним или статистическим факторам следует отнести влияние периода

	Рис. 3.1. Блок-схема алгоритма расчёта параметров и значений плотности распределения мотивируемых потребителями цен на товар

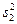временного интервала и влияние числа количественных интервалов, определяемых вариантом данной серии. В качестве сравнительного параметра, осуществляющего оценку факторов влияния, было принято дисперсионное отношение двух сравниваемых массивов данных (наблюдаемого и полученного путём аппроксимации данных):

при 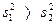, (3-2)

где

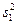- дисперсионная оценка одного массива с большим числовым значением [243, с. 356-358];

- дисперсионная оценка другого сравниваемого массива с меньшим числовым значением [243, с. 356-358].

Рассматривая типичный вариант статистической серии 2 таблицы 3.1, можно выделить, в соответствии с числовыми значениями сравнительного параметра дисперсионной оценки 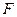, три следующие зоны влияния факторов (рис. 3.2):

- влияние малых интервалов (внутренний фактор);

- влияние малого числа интервалов (внутренний фактор);

- влияние транспортного фактора (внешний фактор), а также зону относительной стабилизации параметров.

Указанные на рис. 3.2 зоны, выявленные путём подсчёта сравнительного параметра дисперсионной оценки 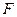, присущи в большей или меньшей степени каждой из исследуемой серии, число которых достигает сорока трёх (табл. 3.1).

Дата добавления: 2015-08-10