Относительная цена мотивации и стандартное распределение мотивационного поведения потребителей.

Поскольку отношение цен мотивации: средней и наивероятнейшей приводит к существенным упрощениям, следует ожидать, что и отношение текущей мотивационной цены к указанной наивероятнейшей цене также позволит в целом упростить применение вероятностного распределения (4-4) в части наличия в распределении характеристик, связанных с проявлением свойств большей универсальности, необходимых для практического применения. Поэтому представляется возможным введение понятия относительной цены мотивации, которая определена как

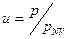, (4-44)

где

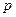- текущая цена мотивации, мысленно назначаемая потребителями за товар.

Учитывая значение наивероятнейшей цены в (4-42), получаем:

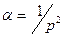, (4-45)

а используя распределение (4-4), можно получить закономерность в виде плотности распределения относительных цен:

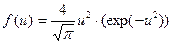, (4-46)

в которой функция (4-46) зависит только от значений относительной мотивируемой потребителями цены 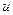. Вывод распределения (4-46) приведен ниже.

Введение понятия относительной цены мотивации определено как

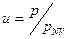, (4-47)

где

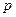- текущая цена мотивации, мысленно назначаемая потребителями за товар.

Учитывая значение наивероятнейшей цены в (4-42), получаем:

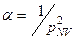, (4-48)

используя распределение (4-4), можно записать:

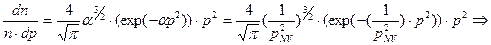
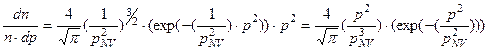. (4-49)

Из (4-44) следует, что

или 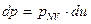. (4-50)

Подставив (4-50) в (4-49), получим:

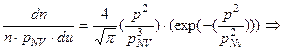(4-51)

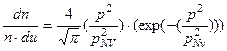. (4-52)

Применив (4-47), получаем вероятное распределение для относительных цен мотивации в виде:

.

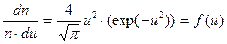Выражение (4-46) и представляет распределение относительных и мысленно мотивированных цен, зависящих от отношения цен 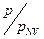, позволяющих создать универсальность.

Аналогичное распределение можно вывести в одномерном координатном измерении, например, для Х -компоненты цены, как проекции относительной цены на ось Х, которую можно определить в виде

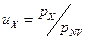. (4-53)

Используя (4-53) в описанном выше выводе, можно получить функцию распределения относительных цен в проекции на ось Х, которая будет:

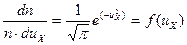. (4-54)

Полученные выражения (4-46) и (4-48) позволяют рассчитать таблицу этих стандартных распределений, задавая для расчёта только величины относительных цен в постоянным шагом изменения в пределах рассчитываемого диапазона, начиная от значения .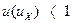

В представленной таблице 4.1 приведены стандартные распределения для относительных цен и их проекций 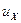на ось Х в диапазоне изменений от 0,02 до 0,98.

Таблица 4.1

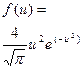
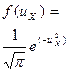
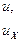
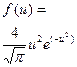
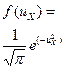
(1)	(2)	(3)		(1)	(2)	(3)
0.02	0.0009	0.5640		0.52	0.4656	0.4305
0.04	0.0036	0.5633		0.54	0.4916	0.4215
0.06	0.0081	0.5622		0.56	0.5172	0.4123
0.08	0.0143	0.5606		0.58	0.5423	0.4030
0.10	0.0223	0.5586		0.60	0.5668	0.3936
0.12	0.0320	0.5561		0.62	0.5906	0.3841
0.14	0.0437	0.5532		0.64	0.6137	0.3746
0.16	0.0563	0.5499		0.66	0.6359	0.3650
0.18	0.0709	0.5462		0.68	0.6572	0.3553
0.20	0.0867	0.5421		0.70	0.6774	0.3456
0.22	0.1041	0.5375		0.72	0.6966	0.3360
0.24	0.1227	0.5326		0.74	0.7147	0.3263
0.26	0.1426	0.5273		0.76	0.7316	0.3166
0.28	0.1636	0.5216		0.78	0.7472	0.3070
0.30	0.1856	0.5156		0.80	0.7616	0.2975
0.32	0.2086	0.5093		0.82	0.7746	0.2880
0.34	0.2327	0.5026		0.84	0.7863	0.2786
0.36	0.2569	0.4956		0.86	0.7967	0.2693
0.38	0.2821	0.4883		0.88	0.8056	0.2601
0.40	0.3077	0.4808		0.90	0.8132	0.2510
0.42	0.3337	0.4729		0.92	0.8194	0.2420
0.44	0.3600	0.4649		0.94	0.8241	0.2332
0.46	0.3865	0.4566		0.96	0.8275	0.2245
0.48	0.4130	0.4481		0.98	0.8295	0.2159
0.50	0.4394	0.4394		1.00	0.8302	0.2075

Применение стандартного распределения общеизвестно из повсеместного его использования в технике статистических вычислений [243] и, применительно к мотивационному поведению потребителей изложено в следующих параграфах.

Дата добавления: 2015-08-10