Параметра распределения .

Исследования, представленные в предыдущем параграфе, указывают на существенную значимость для вычислений параметра распределения 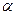, который подлежит определению. Для этого необходим статистический сбор данных с последующей их обработкой. При этом функция , используемая для аппроксимации, определяется согласно выражению, где независимые переменные определяются путём статистического опроса потребителей, то есть

, (4-55)

где

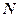- общее количество потребителей в принятом нами единице объёма маркетингового пространства мотивации;

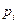- выбранный диапазон изменения мотивационной цены, в пределах которого мысленно назначенная цена соответствует количеству потребителей .

В результате выборочного опроса статистически представительного числа потребителей 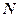и выделения из них количества , назначивших цену , представляется возможным вычислить по формуле (4-55) значения функции распределения , соответствующей мотивируемой потребителями цене 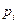. При этом, статистическая представительность числа потребителей в единице объёма пространства может быть достигнута путём выбора представительного числа из таблицы достаточно больших чисел с заранее заданной ошибкой. [243].

Тогда полученные экспериментальные данные вида:

Таблица 4.2

   

 

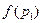
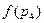
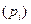
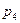
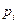
позволяют далее аппроксимировать эти данные методом наименьших квадратов при помощи функции:

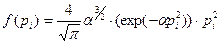, (4-56)

где

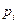и соответствуют значениям таблицы 4.2.

Аппроксимируя данные таблицы 4.2 методом наименьших квадратов с использованием (4-56), можно получить оптимальные коэффициент для 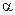в (4-56) с точки зрения минимума суммарного квадратичного приближения параметров функции (4-56) к статистическим данным. Это позволит далее использовать оптимальный параметр 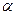для вычисления рассматриваемых средней, наивероятнейшей и относительной цен, связанных с их мотивацией потребителями. Вывод соотношений, связанных с числовым расчётом оптимального коэффициента 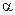для аппроксимирующей теоретической регрессии в соответствии с (4-56), приведен ниже.

Функция , используемая при аппроксимации, определяется согласно выражению, где независимые переменные определяются путём статистического опроса потребителей, то есть

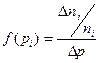, (4-57)

где

- общее количество потребителей в принятом нами единице объёма маркетингового пространства мотивации (эта величина выбирается таким образом, чтобы путём умножения её на объём маркетингового пространства получить общее число потребителей ;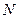

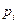- выбранный диапазон изменения мотивационной цены, в пределах которого мысленно назначенная цена соответствует количеству потребителей .

В результате выборочного опроса статистически представительного числа потребителей и выделения из них количества , назначивших цену , представляется возможным вычислить по формуле (4-57) значения функции распределения , соответствующей мотивируемой потребителями цене 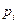. При этом, статистическая представительность числа потребителей в единице объёма пространства может быть достигнута путём выбора представительного числа из таблицы достаточно больших чисел с заранее заданной ошибкой [243].

Тогда полученные экспериментальные данные вида:

Таблица 4.3

   

 

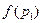
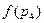
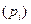
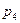
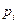
Позволяют далее аппроксимировать эти данные методом наименьших квадратов при помощи функции:

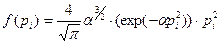, (4-58)

где

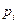и соответствуют значениям таблицы 4.3.

Аппроксимируя данные таблицы 4.3 с использованием (4-57), можно получить оптимальные коэффициенты для (4-58) с точки зрения минимума суммарного квадратичного приближения параметров функции (4-58) к статистическим данным. Это позволит далее оптимизировать полученные коэффициенты таким образом, чтобы получить оптимальный параметр 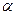, необходимый для вычисления рассматриваемых средней, наивероятнейшей и относительной цен, связанных с их мотивацией потребителями.

Для указанного сделаем в (4-58) замену переменной:

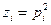(4-59)

и приведём (4-58) к линейному виду путём логарифмирования [56, 25]:

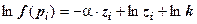, (4-60)

где

Оптимизация методом наименьших квадратов сводится к образованию функции как суммы разностей квадратов между статистическим или экспериментальными значениями в соответствии с табл. 4.3 и теоретическими значениями в соответствии с (4-60) [56, 68, 89, 243], то есть

. (4-61)

Тогда оптимум определяет условие

(4-62)

и, следуя (4-61), имеем

. (4-63)

После преобразования (4-63) получаем уравнение

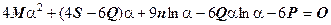, (4-64)

где

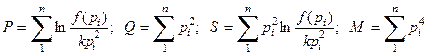, (4-65)

которое решается относительно 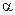известными численными методами [56, 243, 305] (см. Главу 5).

Полученный параметр 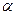позволяет получить среднюю и наивероятнейшую цены мотивации; при этом параметр 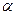можно рассчитать известными статистическими методами с использованием приведенных методологических рекомендаций.

Дата добавления: 2015-08-10