Определение стоимости проекта

Общая стоимость проекта зависит от стоимости выполнения каждой операции, а так же от любых дополнительных переменных или постоянных расходов. Можно снижать длительность выполнения некоторых работ за счет использования дополнительных ресурсов. Если работа лежит на критическом пути, то ее сокращение ведет к сокращению срока реализации проекта. Наименьший возможный срок, к которому может быть завершена работа, называется – критическим сроком выполнения работы. Уменьшение сроков выполнения проектов преследует две основные цели:

1. Минимизация общего времени выполнения проекта.

2. Минимизация общей стоимости проекта.

Минимизация общей продолжительности проекта с минимальными дополнительными расходами является наиболее общей целью оптимизации проекта.

Для решения задачи оптимизации календарного плана проекта необходимо знать стоимость выполнения работ при стандартном и критическом сроках ее выполнения:

Операция	Предшествующая операция	Стандартное значение	Критическое значение
Время	Стоимость	Время	Стоимость
A	-
B	-
C	-
D	A,B
E	B,C
F	C
G	D,E
H	F,G
Сумма		Сумма

Кроме того, дополнительные издержки составляют 1000 в день. Таким образом, стандартная стоимость проекта составляет: 82500+39*1000=121500

Для расчета возможной экономии времени выполнения проекта необходимо провести расчет критического пути проекта, используя критические значения времени выполнения работ.

А

В

С

E

D

G

F

H

При просмотре проекта оговаривается, возможно, изменение критического пути или нет.

Критическая стоимость: 102750+28000=13750

Стоимости: 130750-121500=9250

Результаты расчёта критических сроков и стоимости выполнения проекта показывают, что при использовании критических значений длительность выполнения проекта сокращается примерно на 25%, при этом увеличение стоимости проекта составляет менее 10%: 9250-5000=4250

Учет неопределенности сроков выполнения работ при календарном планировании.

На практике определение точных сроков выполнения работ всегда затруднительно. Однако с помощью экспертных и нормативных методов может быть определено для каждой работы оптимистическое, пессимистическое и наиболее вероятное время ее выполнения.

Нормативные методы используются для определения оптимистического (минимального) срока выполнения работы, а экспертные методы используются для определения наиболее вероятного и пессимистического срока выполнения проекта.

Алгоритм учета неопределенности, получивший наибольшее распространение называется методом оценки и пересмотра проектов.(Project Estimation and Review Technique – PERT).

Одним из наиболее известных методов анализа неопределенности является PERT-анализ.

В основе метода PERT положена предпосылка, что время выполнения каждой отдельно взятой операции проксимируется распределением. Если это верно, то распределение времени выполнения проекта в целом является нормальным. Метод PERT может применятся при анализе конкретного проекта только в случае выполнения данной предпосылки.

a m b

Буквой a – обозначается оптимистический фактор выполнения операции.

b – это пессимистический срок выполнения операции.

m – наиболее вероятное время выполнения операции (математическое ожидание).

Ожидаемая продолжительность операций определяется следующим образом:

t =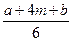

Дисперсия ожидаемой продолжительности определяется по следующей формуле:

σ

Время выполнения проекта можно найти непосредственно по графе, используя для этого ожидаемые значения продолжительности операций.

В предположении, что сроки выполнения операций не зависят друг от друга среднее значение нормального распределения определяется как сумма математических ожиданий продолжительности критических операций, а дисперсия – как сумма их дисперсий.

Полученное нормальное распределение можно использовать для оценки вероятности завершения проекта к заранее установленной дате.

Алгоритм метода PERT:

1. Составить список операций входящих в проект с указанием непосредственно предшествующих работ, оптимистического, наиболее вероятного и оптимистического сроков их выполнения.

2. Построить сетевой граф.

3. В предположении, что время выполнения любой операции аппроксимируется распределением, оценить для каждой операции время ее выполнения и ее дисперсию.

4. Используя ожидаемые значения сроков выполнения операций, найти продолжительность проекта в целом.

5. Определить критические операции и критический путь.

6. С помощью значений дисперсий критических операций определить дисперсию продолжительности всего проекта.

Работы	Непосредственно предшествующая операция	Сроки выполнения операции (недель)
a	m	b
A	-	1.5		2.5
B	A		2.5
C	-
D	C	1.5		2.5
E	B,D	0.5		1.5
F	E
G	B,D		3.5
H	G
I	F,H	1.5		2.5

Операция	Ожидаемый срок выполнения (недель)	Дисперсия
A
B		0.44=
C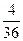
D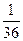
E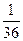
F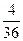
G
H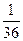
I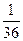

Взаимосвязь названных выше целевых групп может быть представлена в виде треугольника целей проекта

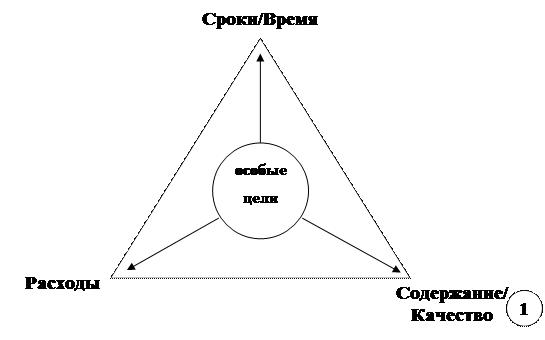Какой из целевых групп будет отдано предпочтение, зависит от каждого отдельного проекта. Кроме того, в процессе работы над проектом приоритеты могут меняться. Чаще всего на первом месте стоят предметные цели, остальные цели носят подчиненный характер.

Анализ и упорядочение целей ориентированных на выполнение проектов, как правило, ведет к выполнению перечня проблем реализации проекта.

При этом формируется план решения проблем, выполнение которого ведет к лучшей мотивации сотрудников, т.к. успех работы виден уже на ранней стадии реализации проекта. Т.е. возникает ощущение реализуемости проекта входе его выполнения, а не через несколько лет.

Дата добавления: 2015-08-10