Разложение несинусоидального U в ряд Фурье.

На практике приходится иметь дело не с синусоидами, а с более или менее сложными искажен кривыми. Затем даже при синусоид э.д.с. форма кривой тока может резко отличаться от синусоиды как из-за изменения актив сопротивления (например, если в цепь введена вольтова дуга), так и из-за изменения реактив соп-я (например, если в цепи имеется индукцион катушка с насыщ железным сердечником). Таким образом, периодич несинусоид токами и U называют токи и U, изменяющиеся во времени по периодич несинусоидал закону.

Явления, происходящие в цепях с несинусоид э.д.с, проще всего поддаются исследованию, если несинусоид э.д.с, изменяющся периодически, разложить на синусоиду с таким же числом периодов, как и кривая э. д. с, и на ряд высших гармонических синусоид, число периодов k в 2, 3, 4, 5... раз ↑ числа периодов основной синусоиды. Фурье показал, что всякую конечную периодич функцию, удовлетв условиям Дирихле, т. е. получающую ч/з = промежутки времени те же значения, f(wt)= f[(wt+Т)] или f(a)=f(a+2p),

непрерывную и периодич, можно разложить в ряд синусоид функций

Синусоида A₁sin(x+y₁) считается основной, а остальные, например, A ₇sin(x+y₇) высшей гармонической точкой седьмого порядка.

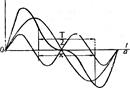
Такие периодические эдс, напряжения и токи можно представить в виде рядов Фурье, которые в общем случае содержат постоянную составляющую, основную или первую гармонику, имеюшую период, равный периоду самой функции, и высшие гармоники, частота которых в целое число раз больше частоты первой гармоники. Например, для периодической эдс можем написать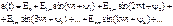

Дата добавления: 2015-07-20