Метод узловых потенциалов (символич. форма)

Пример:В тех случаях, когда источниками энергии в цепи являются источники токов и когда число узлов хотя бы на 2 узла ↓, чем число независимых контуров, предпочтительнее пользоваться для расчета I в сложной цепи методом уз. потц. Этот метод сохраняет только те ур-я Кирхгофа, k составлены для узлов, и исключить ур-я для контуров. В качестве вспомогат. неизвестных при расчете цепей методом уз.п. вводятся потцы узлов цепи относительно 1 из них – опорного узла. Потц опорного узла φ₀=0. Потцы д.р. узлов относит опорного обозначим через φ₁, φ₂ и т. д. Далее составляем ур-я для токов в ветвях на основании обобщенного закона Ома:

,

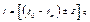где g – проводимость.

Составляем систему уравнений:

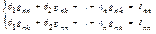
Где g_nn- сумма провод-тей ветвей, сходящихся в узле. g_nk- сумма провод-тей ветвей, соедин. узлы k и n, взятая со знаком -. Если ветви меж узлами нет g=0. I_NN - узловой ток = геом. сумме частного Э.Д.С. ветвей сходящихся в контуре к их сопротив с учетом направления этих ЭДС

Решаем систему и подставив в ур-я токов φ₀ и φ_n найдем токи в ветвях.

82.83. Расчет трехфазных цепей (∆ / Y). (Симметрич нагрузка).

В простейшем случае симметрич режима работы 3фазной цепи, когда гентор и нагрузка соединены Y (рис. 4.9,а), векторная диаграмма э. д. с. и токов показанны на рис.

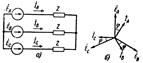
Ток в k фазе отстает от э. д. с. той же фазы на угол j=arctg x/r, где г и х - актив и реактив сопротивл фаз.

Ток в фазе А находят так же, как в 1фазной цепи, потому что нейтрал точки гентора и нагрузки в симетрич режиме могут быть соединены, как имеющие одинаковые потенциалы: IА=EA/Z

Токи в фазах В и С выртся ч/з ток IA IB=a²IA, IC=aIA наличие нейтрал провода не вносит при сим режиме никаких изменений, так как сумма токов 3 фаз равна 0 и ток в нем отсутствует → при симном режиме работы 3фазной цепи задача сводится к расчету 1 из фаз аналогично расчету 1офазной цепи. При этом Z нейтрального провода не учитывается, так как I в нем и → падение U на нем отсутствуют.

В случае соединения ∆ линейные токи определяются в соответствии с 1 законом Кирхгофа как разность фазных токов, и при симном режиме соблюдается соотношение I_л= Ö3I_ф. Соединение фаз генератора или нагрузки ∆ должно быть для расчета заменено эквивал соединением фаз Y; вследствие этого расчет 3фазной цепи с соединением фаз ∆ приводится в конечном итоге к расчету эквивал 3фазной цепи с соединением фаз Y.

Между сопротивлениями сторон ∆ (Z_D) и лучей Y (Z_Y) имеет место соотношение Z_Y = Z_D/3, вытекающее из формул преобразования ∆ соп-ний в эквивал Y. Это справедливо как для соп-ний симметрич 3фазной нагрузк, так и для сопний симметрич 3фазного гентора. При этом фазные э.д.с. Э.Г., соединенн Y, берутся в Ö3 раз ↓ фазных э. д. с. заданного гентора, соединенного ∆ (кроме того, они должны быть сдвинуты на угол 30°). Это вытекает из векторной потенциаль диаграммы U генора.

84. Расчет 3фазных цепей (Y /Yс 0). (Несимметричный режим).

Несимметрич 3фазная цепь, соедная Y, с нейтрал проводом

Несим 3фазная цепь может смотреться как 3контурная цепь с 3 э.д.с. Такая цепь может быть рассчитана методом кон токов, уз U и другими методами. Поскольку в схеме имеются только 2 узла, наиболее целесообразно в данном случае определить узловое U (U смещения) между нейтрал точками О' и О по формуле:

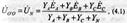
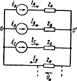
где Y_A, Y_B, Y_C, Y_N - проводимости соответствующих ветвей.

После этого найдем токи:

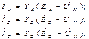
При отсутствии нейтрал провода, полагая в Y_N =0. имеем:

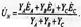
85. Расчет 3фазных цепей (∆ / ∆). (Несимметрич режим).

Несим 3фазная нагрузка, соединен ∆, с заданными U на зажимах

Если на зажимах несим 3фазной нагрузки, соединенной ∆, заданы линейные U 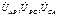, то токи в сопях нагрузки равны 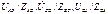Токи в линии определяются как разности соответствующих токов нагрузки:

например, и т. п.

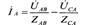
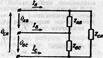
Если на зажимах несим 3фазной нагрузки, соединенной ∆. Заданны фазные UA,UB,Uc источника, соединенного в Y, то линейные U на зажимах нагрузки находятся как разности соответствующих фазных U, в результате чего задача сводится к только что рассмотренному случаю.

Дата добавления: 2015-07-20