Понятие о напряжениях, деформациях и перемещениях. Нормальные и касательные напряжения. Вектор полного перемещения. Линейная и угловая деформация

Напряжение – численная мера распределения внутренних сил по плоскости поперечного сечения. Его используют при исследовании и определении внутренних сил любой конструкции.

Выделим на плоскости сечения площадку DA; по этой площадке будет действовать внутренняя сила DR (рис. I.1.10 а).

Величина отношения DR/DA=p_ср называется средним напряжением на площадке DA. Истинное напряжение в точке А получим устремив DA к нулю:

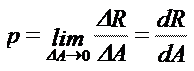
Нормальные напряжения возникают, когда частицы материала стремятся отдалиться друг от друга или, наоборот, сблизиться. Касательные напряжения связаны со сдвигом частиц по плоскости рассматриваемого сечения.

Очевидно, что 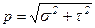. Касательное напряжение в свою очередь может быть разложено по направлениям осей x и y (t_zх, t_zу). Размерность напряжений – Н/м² (Па).

При действии внешних сил наряду с возникновением напряжений происходит изменение объема тела и его формы, т. е. тело деформируется. При этом различают начальное (недеформированное) и конечное (деформированное) состояния тела.

Отнесем недеформированное тело к декартовой системе координат Oxyz. Положение некоторой точки М в этой системе координат определяется радиус-вектором r(х, у, z). В деформированном состоянии точка М займет новое положение М^/, характеризуемое радиус-вектором r ' (х, у, z). Вектор u=r'—r называется вектором, перемещений точки М.

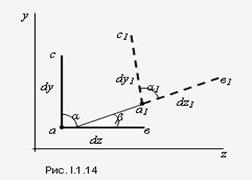
Под действием внешних сил любое тело деформируется, т.е. его форма и размеры изменяются, а точки тела меняют положение в пространстве. Пусть имеется тело с приложенными к нему силами Р_i. Мысленно через точку а в направлениях осей у и z проведем бесконечномалые отрезки ав и ас, длины которых dy и dz. После деформации бруса отрезки примут положение, изображенное штриховой линией (рис. I.1.14). Точка а переместится в положение а₁. Величина аа₁, равная изменению координат точки называется линейным перемещением точки а. Отрезки ав и ас займут новые положения а₁в₁ и а₁с₁. Их длины изменяются на Δdy и Δdz и называются абсолютными линейными деформациями. Угол между начальным положением отрезка ав и конечным - а₁в₁ - называются угловым перемещением b. Линейные перемещения измеряются в единицах длины, угловые - в радианах или градусах. Отношение приращения длины отрезка к его начальной длине представляет собой относительную линейную деформацию, т.е. . Аналогично .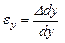

Линейные деформации величины безразмерные. Изменение первоначально угла между отрезками ав и ас после приложения к телу нагрузки, выраженное в радианах, представляет собой угловую деформацию .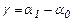

Совокупность линейных деформаций e по различным направлениям и угловых деформаций g по различным плоскостям, проходящим через рассматриваемую точку, представляет собой деформированное состояние в этой точке.

Дата добавления: 2015-07-25