Механические хар-ки. Диаграмма растяжения.

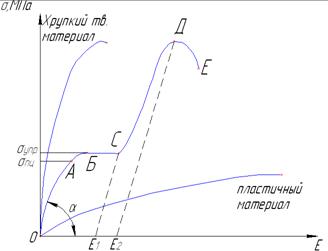
На диаграмме растяжения фиксир-ся растяжение конкретного материала до его полного разрушения, с целью оценки характерных механич. хар-к материала. Деформация исследуется для упругопластичного материала (н-р, малоуглерод.сталь)

Т. А соот-ет предел пропорциональности (это максимальное напряжение до которого материал соответствует закону Гука): σ_пц=F_пц/S.

Т. Б соот-ет предел упругости (это такое максимальное напряжение, при кот. после снятия нагрузки материал вернётся в исходное состояние): σ_упр=F_упр/S. Область упругих деформаций.

Т. С соот-ет предел текучести (это такое напряжение, при кот. без видимого изменения нагрузки материал течёт). Если снять нагрузку, то материал вернётся в положение Е₁. Область остаточных деформаций.

После т. С необходимо приложить дополнит. силу до т. Д – это зона упрочнения. Т. Д – временный предел прочности (максимальное напряжение, при кот. материал не разрушается). Если снять нагрузку в т. Д, то материал вернётся в положение Е₂, и его использовать нельзя.

Т. Е – разрушение образца.

Tgα – модуль упругости.

Механич. св-ва материала:

- Прочность – способность не разрушаться под нагрузкой;

- Жёсткость – способность незначительно деформироваться под нагрузкой;

- Выносливость – способность долгое время выдерживать переменные нагрузки;

- Устойчивость – способность сохранять первоначальную форму упругого равновесия;

- Вязкость – способность воспринимать ударные нагрузки.

Характеристики материалов:

- Твёрдость;

- Хрупкость;

- Пластичность.

Допущения о свойствах материалов:

Однородные – в люб. точке материалы имеют одинак. физико-химич. св-ва;

Сплошная среда – кристаллич. строение и микроскопич. дефекты не учитываются;

Изотропны – механич. св-ва не зависят от направления нагружения;

Идеальная упругость – полностью восстанавливают форму и размеры после снятия нагрузки.

Дата добавления: 2015-07-25