Метод сечения, виды внутренних силовых факторов.

Для выявления внутренних сил в сопротивлении материалов применяется метод сечения.

Суть метода: рассекаем тело плоскостью; мысленно отбрасываем наиболее нагруженную часть тела (1); действие отброшенной части тела на оставшейся части замещаем равнодействующими внутренних силовых факторов и приводим их в центр тяжести поперечного сечения. Поперечное сечение – это сечение, плоскость которого перпендикулярна оси тела. Главные векторы сил эквивалентны действию отброшенной части на оставшуюся часть. При этом оставшаяся часть тела нах-ся в равновесии. Ур-ние равновесия: .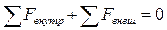

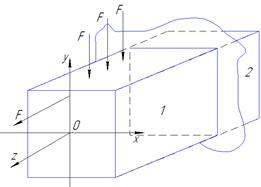
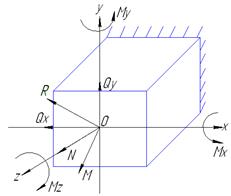
Разложив главный вектор R и главный момент M на составляющие по осям, получим силы N, Qx, Qy, и моменты Mx, My, Mz, которые называются внутренними силовыми факторами. Шесть внутр.силовых факторов вместе с известными внеш.силами на оставшейся части тела образуют уравновешенную сис-му сил, для кот. можно составить 6 ур-ний равновесия.

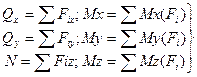
N – нормальная (продольная) сила;

Qx, Qy – поперечные силы;

Mz – крутящий момент;

Mx, My – изгибающие моменты.

Растяжение. Основные понятия, допущения и зависимости.

Растяжение – это такой вид нагружения, когда в поперечном сечении растянутого тела действуют только продольные силы N. Прямой брус, работающий на растяжение, наз-ся стержнем.

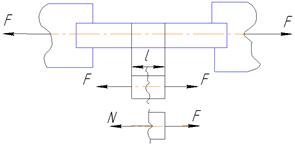
Согласно методу сечений рассечём растянутый стержень и отбросим его левую часть, то для уравновешивания внешней силы F (равнодействующая сис-ма сил крепления образца) достаточно в сечении приложить только один внутренний силовой фактор – нормальную силу N.

N=F – условие равновесия. Остальные внутренние силовые факторы в данном случае равны 0. При растяжении стержень нах-ся в напряжённом состоянии. Напряжение при растяжении σ=N/S, где S – площадь поперечного сечения. Нормальное напряжение направлено также как и нормальная сила.

Ряд допущений:

- по всей длине участка действ. внутр. сила;

- внутр. сила по попереч. сечению распределена равномерно;

- по всей длине участка l значение деформации ∆ l и Е постоянны.

Если в рез-те алгебраич-го сложения проекций внешних сил получилось, что N>0, то нормальная сила направлена от сечения и стержень в этом сечении испытывает растяжение; иначе стержень испытывает сжатие.

Если стержень нагружен большим числом осевых сил направленных в противоположные стороны, то применяется правило знаков при определении нормальной силы: проекции внешних сил, направленных от сечения, положительны и, наоборот.

При переходе от одного сечения к другому нормальная сила изменяется, поэтому строят графики изменения значения нормальной силы N по длине бруса, кот. наз-ся эпюрами.

Растяжение, закон Гука. Основные понятия и зависимости, влияние на абсолютное удлинение стержня.

Растяжение – это такой вид нагружения, когда в поперечном сечении растянутого тела действуют только продольные силы N.

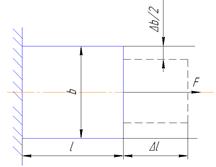
Рассмотрим деформацию бруса под действием продольной силы. l – начальная длина, b – начальная ширина, ∆ l – абсолютное удлинение, ∆b – абсолютное сужение.

Относительная продольная деформация Ε:

Ε=∆l/l.

При растяжении тела происходит изменение его поперечного сечения, т.е. сужение. Линейная (поперечная) деформация:

Ε₁=∆b/b.

Данные деформации учитывают в точных расчётах.

μ =Ε1/Ε – коэф-т относительной деформации, или коэф-т Пуассона, - хар-ка пластичности материала.

В пределах упругих деформаций между нормальным напряжением и продольной деформацией сущ-ет прямопропорциональная зависимость (Закон Гука): σ= Ε Ε, где Е – модуль упругости (модуль Юнга), хар-ет жёсткость материала, т.е. сопсобность сопротивляться деформациям, Па.

Так как σ=F/S, то получим зависимость между нагрузкой, размерами стержня и возникающей деформацией: F/S= Е ∆l/l, откуда ∆l= F l/ Е S. Произведение Е S наз-ют жёсткостью сечения. Следовательно, абсолют. удлинение стержня прямо пропорционально вел-не продольной силы в сечении, длине стержня и обратно пропорционально площади поперечного сечения и модулю упругости.

Определение деформации стержня под нагрузкой и сравнение её с допускаемой наз-ют расчётом на жёсткость. А также проводят расчет на прочность стержня.

Дата добавления: 2015-07-25