Задача коммивояжера

Имеется n городов. Выезжая из исходного города А₁, коммивояжер должен побывать во всех остальных городах по одному разу и вернуться в город А₁.

Задача заключается в определении последовательности объезда городов, при которой коммивояжеру требуется минимизировать некоторый критерий эффективности: стоимость проезда, время в пути, суммарное расстояние и т.д. Пусть задана матрица C=||c_ij|| расстояний между городами и требуется минимизировать суммарную длину пути.

Введем переменные

x_ij=1, если коммивояжер переезжает из города А_i в город А_j, i j;

x_ij=0, в противном случае,

.

Математическая модель задачи выглядит следующим образом.

Целевая функция имеет вид:

.

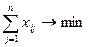ЦФ представляет суммарную длину пути.

Ограничения имеют вид:

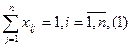
где u_i, - неограниченные действительные переменные.

Условия (1) означает, что коммивояжер выезжает из каждого города один раз, а условия (2)- что он въезжает один раз в каждый город.

Условия (3), выглядящие несколько искусственно, предназначены обеспечить связность маршрута коммивояжера. Более точно эти условия запрещают любой цикл, не проходящий через город 1, и тем самым исключают ситуации, подобные приведенной на рисунке 4.20.

Рис. 4.20

Дата добавления: 2015-07-21