Пример 4.3

На рис. 4.10 дано изображение неориентированного графа, справа от него соответствующая матрица смежности.

Рис. 4.10 Неориентированный граф и соответствующая ему матрица смежности

Маршрутом S в графе G называется конечная последовательность ребер , вида , для которой 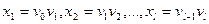. Число ребер в маршруте называется длиной маршрута.

Маршрут, в котором нет повторяющихся ребер, называется цепью.

Вообще цепь – это чередующаяся последовательность вершин и ребер (v₀, x₁, v₁, x₂, …, v_k-1, x_k, v_k), где v_i-1 и v_i являются концами ребра x_i. В компактной форме эта запись выглядит так: (v₀, v₁, …, v_k-1, v_k) или (x₁, x₂, …, x_k). В отличие от простой цепи, цепь общего вида может содержать повторяющиеся вершины. Обычно цепь рассматривается не как самостоятельный граф, а как часть некоторого другого графа. Длиной цепи называют количество составляющих ее ребер. Ясно, что длина простой цепи не может превышать порядок содержащего ее графа, а длина цепи общего вида – числа ребер этого графа.

Понятие цепи широко используется в теории графов. Например, связный граф можно определить как граф, в котором любая пара вершин соединена хотя бы одной цепью.

Если в цепи совпадают начальная и конечная вершины (замкнутая или простая цепь), то такая цепь называется циклом (простым циклом). В общем случае граф, представляющий собой простой цикл, обозначается как С_n. Основной интерес, как и в случае цепей, представляет рассмотрение циклов не как самостоятельных графов, а как частей некоторого графа.

Рис. 4.11 Пример цепи и простого цикла

Цепи и циклы называются простыми, если в них нет повторяющихся вершин. Две вершины u, v называются связанными, если существует маршрут S, в котором концами являются u и v. Граф называется связным, если в нем любые вершины связаны. Связный граф без циклов называется деревом (см. рис. 4.12).

Рис. 4.12 Примеры деревьев

Совокупность k деревьев называется k–лесом.

Деревья являются простым, но очень важным видом графов. С их помощью легко описывается структура самых различных объектов: организаций и учреждений, книг и документов, математических формул, химических соединений, компьютерных файловых систем, программ и многое другое.

Считается, что первым использовал понятие дерева Кирхгофф в 1847 г. при исследовании электрических цепей. Спустя десятилетие химик Кэли ввел термин «дерево» при изучении структуры углеводородных соединений и получил первые важные результаты в этом разделе теории графов.

На рис. даны изображения одного и того же неориентированного дерева. Наиболее соответствует названию вариант в, но обычно при изображении деревьев используются варианты а и б. Из рисунка становятся понятными термины корень и лист, употребляемые при рассмотрении подобных графов. Листом (висячей вершиной) называют вершину, степень которой равна 1, если она не рассматривается как корень. В качестве корня в неориентированном дереве можно принять любую вершину.

Существует несколько эквивалентных определений неориентированного дерева, каждое из которых отражает различные свойства последнего. Приведем некоторые из них.

1) Дерево – это связный граф без циклов.

2) Дерево – это граф, в котором любая пара вершин связана единственной цепью. (Действительно, наличие двух и более цепей, соединяющих некоторую пару вершин, означает присутствие циклов, образованных несовпадающими частями таких цепей).

3) Дерево – это связный граф, имеющий n вершин и n-1 ребер.

Теорема 3. Пусть дан граф G(V, X) с матрицей смежности А. Тогда (i, j)–й элемент матрицы Аⁿ равен числу маршрутов длины n из v_i в v_j.

Теорема 4. (Матричная теорема о деревьях). Пусть G связанный граф с матрицей смежности А. М – матрица, полученная из А заменой i-го элемента главной диагонали на deg(v_i). Тогда все алгебраические дополнения матрицы М равны между собой и их общее значение равно числу остовов G.

Дата добавления: 2015-07-21