Читайте также:
|
На рис. 4.9. дано изображение ориентированного графа и приведена соответствующая ему матрица инциденций
Рис. 4.9 Ориентированный граф и соответствующая ему матрица инциденций
Определим матрицу смежности как симметричную квадратную матрицу А={ai,j} порядка n, в которой элемент ai,j равен 1, если в графе есть ребро {vi, uj }, т.е. vi и uj смежны, и 0, если такого ребра нет.
Из определения следует, что 
при любом i, 
при любом j и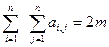 
, т.е. количество единиц в любой строке или столбце матрицы смежности равно степени соответствующей вершины графа, а общее количество единиц равно удвоенному числу его ребер.
Так как для неориентированного графа отношение смежности симметрично, то матрица смежности симметрична. Существует взаимно однозначное соответствие между графами с p вершинами и симметричными бинарными p x p матрицами с нулями на диагонали. Суммы элементов по строкам и столбцам неориентированного графа равны степеням соответствующих вершин графа.
Дата добавления: 2015-07-21; просмотров: 58 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Пример 4.1 | | | Пример 4.3 |