Транспортная задача с избытком запасов

В пунктах СК₁, СК_2, …СК_м имеются запасы груза A₁, A₂,..., A_m; пункты МГ₁, МГ₂, …, МГ_N подали заявки B₁, B₂,..., B_n, причем

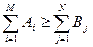, (где i=1,...,m; j=1,...,n)

Требуется найти такой план перевозок (X), при котором все заявки будут выполнены, а общая стоимость перевозок минимальна.

Очевидно, при этой постановке задачи некоторые условия-равенства транспортной задачи превращаются в условия-неравенства, а некоторые — остаются равенствами.

_n

∑X_i,j ≤ А_i (i=1,..., m);

^j=1

_M

∑ X_i,j = В_j (j=1,..., n).

ⁱ⁼¹

Мы умеем решать задачу линейного программирования, в какой бы форме — равенств или неравенств не были бы заданы ее условия. Поставленная задача может быть решена, например, обычным симплекс-методом. Однако задачу можно решить проще, если искусственным приемом свести ее к ранее рассмотренной транспортной задаче с правильным балансом. Для этого, сверх имеющихся n пунктов назначения МГ₁, МГ₂, …, МГ_N, введём ещё один, фиктивный, пункт назначения МГ_N+1, которому припишем фиктивную заявку, равную избытку запасов над заявками:

(где i=1,...,m; j=1,...,n),

а стоимость перевозок из всех пунктов отправления в фиктивный пункт назначения МГ_N+1 будем считать равным нулю. Введением фиктивного пункта назначения МГ _N+1 с его заявкой МГ _N+1 мы сравняли баланс транспортной задачи и теперь его можно решать как обычную транспортную задачу с правильным балансом.

Если требуется обеспечить вывоз всего товара у какого-либо поставщика, то стоимость перевозки товара от этого поставщика фиктивному потребителю принимается равной очень большому числу.

Если требуется распределить излишек товара по всем поставщикам, то запасы товара у всех поставщиков искусственно уменьшаются. Для этого необходимо умножить все величины запасов на коэффициент . Вводить фиктивного потребителя в этом случае не требуется.

Дата добавления: 2015-07-21