
Читайте также:
|
Табличный процессор Ехсеl имеет развитые средства, позволяющие решать разнообразные задачи оптимизации, в том числе задачи линейного и нелинейного математического программирования. Решим задачу из примера 2.1, используя табличный процессор Ехсеl.
Предположим, что желательно получить результаты (значения переменных х1 и х2) в ячейках В2 и С2 (конечно, можно использовать и любые другие ячейки). В ячейках ВЗ и СЗ введем коэффициенты целевой функции (100 и 300). В ячейке DЗ введем формулу целевой функции:
=СУММПРОИЗВ(В3:СЗ;В2:С2)
В ячейках В4 и С4 введем коэффициенты первого ограничения (на расход алюминия): 20 и 5.
В ячейке D4 введем формулу этого ограничения:
=СУММПРОИЗВ(В4:С4;В2:С2)
В ячейке F4 введем правую часть этого ограничения: 200.
Аналогично в ячейках В5 и С5 введем коэффициенты ограничения на расход стали (20 и 5), в ячейке D5 - формулу этого ограничения
(=СУММПРОИЗВ(В5:С5;В2:С2)),
в ячейке F5 - правую часть (250). В ячейках В6 и С6 введем коэффициенты ограничения на расход пластмассы (5 и 20), в ячейке D6 - формулу этого ограничения
(=СУММПРОИЗВ(В6:С6;В2:С2)),
в ячейке F6 - правую часть (500).
Примечание. Вводить описание математической модели в рабочий лист Ехсеl можно и по-другому. Например, для ввода целевой функции достаточно в любой ячейке указать формулу: = 100*В2+300*С2. Для ввода первого ограничения достаточно в одной из ячеек указать формулу = 20*В2+5*С2, а в другой - правую часть ограничения (200). Однако показанный выше способ позволяет при необходимости легко внести изменения в постановку задачи.
Укажем также некоторые поясняющие надписи и обозначения (хотя это и необязательно). Рабочий лист будет иметь примерно такой вид, как показано на рис. 2.3.
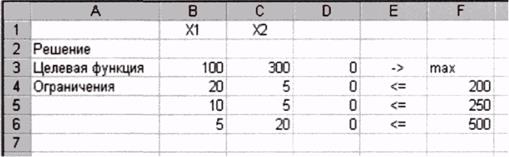
Рис. 2.3. Рабочий лист Ехсеl для решения примера 2.1
Примечание. Подписи и обозначения на рабочем листе (х1, х2,- >, >= и т.д.), показанные на рис. 2.3, необязательны. Значения 0 в ячейках DЗ – D6 получены автоматически для начальных значений переменных, равных нулю.
Для решения задачи из меню «Сервис» выберем элемент «Поиск решения». В поле «Установить целевую ячейку» указывается ячейка D3, где находится формула целевой функции. Используя переключатели, необходимо указать, что требуется установить ячейку DЗ «равной максимальному значению (так как целевая функция в этой задаче подлежит максимизации). В поле «Изменяя ячейки» указываются ячейки, в которых должны находиться значения переменных: В2:С2.
В области «Ограничения» указываются ограничения. Для начала их ввода требуется нажать кнопку «Добавить». На экран выводится окно «Добавление ограничения». В этом окне в поле «Ссылка на ячейку» указывается ячейка, в которой находится левая часть (формула) ограничения, а в поле «Ограничение» - правая часть ограничения (число или ссылка на ячейку, где находится правая часть ограничения). Чтобы задать первое из ограничений (на расход алюминия), требуется в поле «Ссылка на ячейку» указать ячейку D4, выбрать знак ограничения (<=), а в поле «Ограничение» указать ячейку F4. Для ввода ограничения требуется нажать кнопку «Добавить». Аналогично вводятся остальные ограничения. Для ввода ограничения на расход стали требуется в поле «Ссылка на ячейку» ввести D5, в поле знака ограничения - знак <=, в поле «Ограничение» - F5. Для ввода ограничения на расход пластмассы требуется в поле «Ссылка на ячейку» ввести D6, в поле знака ограничения – знак <=, в поле «Ограничение» - F6. Кроме того, требуется ввести ограничение на неотрицательность всех переменных: В2:С2 >=0. Необходимо также указать, что переменные, определяемые в задаче, должны принимать целочисленные значения (так как они обозначают количество изделий). Для этого необходимо в поле «Ссылка на ячейку» указать В2:С2, а в поле знака ограничения выбрать отметку «цел». По окончании ввода всех ограничений требуется нажать ОК.
Для решения задачи следует нажать кнопку «Выполнить». После появления окна с сообщением о том, что решение найдено, следует установить переключатель «Сохранить найденное решение» и нажать ОК. Рабочий лист с результатами решения будет иметь примерно такой вид, как показано на рис. 2.4.
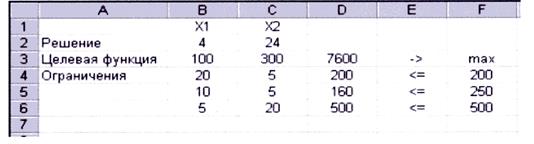
Рис. 2.4. Рабочий лист Ехсеl с результатами решения примера 2.1
В ячейках В2 и С2 получены оптимальные значения переменных, в ячейке DЗ - оптимальное значение целевой функции. Таким образом, за смену цех должен выпускать 4 корпуса и 24 задвижки. Прибыль составит 7600 ден. ед. Эти результаты совпадают с результатами, полученными с помощью графического метода и симплекс-метода.
В ячейках D4, D5 и Dб находятся значения левых частей ограничений (т.е. величины, получаемые при подстановке оптимальных значений переменных в ограничения). В данной задаче эти величины обозначают расход ресурсов. Таким образом, видно, что на выпуск 4 корпусов и 24 задвижек будет израсходовано 200 кг алюминия, 160 кг стали и 500 кг пластмассы.
Дата добавления: 2015-07-21; просмотров: 113 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Определение оптимального решения на основе симплекс-таблиц | | | Анализ оптимального решения на чувствительность |