Приведение задач ЛП к стандартной форме

В общем случае задача линейного программирования записывается так, что ограничениями являются как уравнения, так и неравенства, а переменные могут быть как неотрицательными, так и произвольно изменяющимися.

Для большинства методов решения задач ЛП требуется предварительно привести задачу к стандартной (канонической, нормальной) форме. Задача (или ее математическая модель) представлена в стандартной форме, если она соответствует следующим условиям:

· Целевая функция подлежит максимизации;

· Все ограничения имеют вид равенств;

· На все переменные накладываются ограничения неотрицательности.

Если целевая функция задачи подлежит минимизации, то для перехода к целевой функции, подлежащей максимизации, необходимо умножить исходную целевую функцию на (– 1). Доказано, что максимальное значение любой функции Е всегда равно минимальному значению функции (– Е), взятому с обратным знаком.

Для преобразования ограничения «больше или равно» в равенство (т.е. в ограничение «равно»), необходимо вычесть из левой части ограничения дополнительную переменную. Для преобразования ограничения «меньше или равно» в равенство необходимо прибавить к левой части ограничения дополнительную переменную. На все переменные, используемые для приведения задачи к стандартной форме, накладываются ограничения неотрицательности. Переменные, вычитаемые из ограничений «больше или равно» для их приведения к стандартной форме называются избыточными, а переменные, прибавляемые к ограничениям «меньше ли равно» - остаточными.

Если на какую-либо переменную накладывается ограничение неотрицательности, то она заменяется на разность двух переменных, каждая из которых должна быть неотрицательной. Таким образом, если некоторая переменная x_j по своему физическому смыслу может принимать как положительные, так и отрицательные значения, то во всех ограничениях и в целевой функции ее следует заменить на разность двух переменных: x^’_j – x^”_j. На эти переменные накладываются ограничения неотрицательности: x^’_j 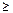0, x^”_j 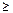0.

Приведем к стандартной форме задачу из примера 1.1. Из ограничений «больше или равно» необходимо вычесть избыточные переменные, к ограничению «меньше или равно» - прибавить остаточную переменную. Целевая функция задачи подлежит максимизации, и на все переменные накладывается ограничение неотрицательности; поэтому никаких других преобразований не требуется. Математическая модель задачи в стандартной форме будет иметь следующий вид:

x₁ – x₃ =200

x₂– x₄ =100

0,5x₁+1,2x₂ +x₅=600

x₁ 0; x₂ 0

Е=25x₁+40x₂→ max

Здесь переменные x₃, x₄ – избыточные, x₅ – остаточная.

Примечание. Все переменные, которые вводятся в математическую модель для ее приведения к стандартной форме, имеют физический смысл. Так, в рассмотренном примере переменные x₃ и x₄ обозначают количество кислот, которое будет выпущено сверх государственного заказа. Переменная x₅ обозначает, насколько количество опасных отходов, образующихся при производстве кислот, будет меньше максимально допустимой величины (600 т).

Приведем к стандартной форме задачу из примера 1.2. В ней имеются три ограничения «больше или равно». В каждое из них необходимо ввести избыточную переменную. Целевая функция задачи подлежит минимизации, ее необходимо умножить на (– 1), чтобы перейти к целевой функции, подлежащей максимизации. Математическая модель задачи в стандартной форме будет иметь следующий вид:

x₁ – x₃ =200

x₂– x₄ =100

25Х₁+40x₂ –x₅=20000

x₁ 0; x₂ 0

–Е= –0,5x₁–1,2x₂ → max.

Дата добавления: 2015-07-21