Теоретическое введение. 2.2.1 Симплекс – (от лат

2.2.1 Симплекс – (от лат. simplex – простой, математический), простейший выпуклый многогранник данного числа измерений n. При n = 3 трёхмерный симплекс представляет собой произвольный, в том числе неправильный, тетраэдр. Под двумерным симплексом понимают произвольный треугольник, а под одномерным - отрезок. Нульмерный симплекс есть просто одна точка.

n -мерный симпекс имеет n + 1 вершин, не принадлежащих ни к какому (n - 1)-мерному подпространству того Евклидова пространства (с числом измерений n или больше), в котором лежит данный симплекс. Обратно, всякие n + 1 точек евклидова n -мерного пространства R^m, m ³ n, не лежащие ни в каком подпространстве менее n измерений, однозначно определяют n -мepный симплекс с вершинами в заданных точках e₀, e₁,..., e_n, он может быть определён как выпуклое замыкание совокупности заданных n + 1 точек, т. е. как пересечение всех выпуклых тел пространства R^m, содержащих эти точки. Если в пространстве R^m дана система декартовых координат x₁, х₂,. .., х_т, в которой вершина e_i, i = 0, 1,..., n, имеет координаты x₁ ⁽ⁱ⁾, x₂ ⁽ⁱ⁾,..., x_m ⁽ⁱ⁾, то симплекс с вершинами e₀, e₁,..., e_m состоит из всех точек пространства, координаты которых имеют вид:

,

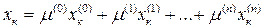k = 1,2, ..., m, где m⁽⁰⁾, m⁽¹⁾,..., m^(п) - произвольные неотрицательные числа, дающие в сумме 1.

По аналогии со случаем n = 3 можно сказать, что все точки симплекса с данными вершинами получаются, если в эти вершины поместить произвольные неотрицательные массы (из которых, по крайней мере, одна отлична от нуля) и взять центр тяжести этих масс (дополнительное требование, чтобы сумма всех масс равнялась 1, исключает лишь случай, когда все массы - нулевые).

Любые r + 1 вершин, 0 £ r £ n - 1, взятые из числа данных n + 1 вершин n -мерного симплекса, определяют некоторый r -мерный симплекс. - r -мерную грань данного симплекса. Нульмерные грани симплекса называются вершинами, одномерные грани – ребрами.

Симплекс-метод позволяет решать задачи линейного программирования любой размерности, т.е. с любым количеством переменных. Решение задач линейного программирования на основе симплекс-метода состоит в целенаправленном переборе угловых точек ОДР в направлении улучшения значения целевой функции.

Можно доказать, что экстремум (минимум иди максимум) целевой функции всегда достигается при значениях переменных х₁,х₂,…,х_n, соответствующих одной из угловых точек ОДР. Другими словами, оптимальное решение всегда находится в угловой точке ОДР.

Дата добавления: 2015-07-21