Порядок выполнения работы. 1. Изучить теоретическую часть.

1. Изучить теоретическую часть.

2. Решить транспортную задачу.

Контрольные вопросы

1. Дайте общую характеристику распределительной задачи.

2. В чем заключается транспортная задача?

3. Почему транспортные задачи нецелесообразно решать симплекс-методом?

4. Назовите этапы решения транспортной задачи.

5. Расскажите принцип метода минимального элемента.

6. Какие переменные называются базисными, а какие небазисными в транспортной задаче?

7. Расскажите принцип метода потенциалов.

8. Назовите условие завершения решения транспортной задачи.

9. Какие транспортные задачи называются задачами с неправильным балансом?

10. Перечислите направления нарушения баланса транспортной задачи.

11. Как решать транспортные задачи с избытком запасов?

12. Как решать транспортные задачи с избытком заявок?

13. В каких случаях получается вырожденное решение?

Лабораторная работа № 4

Основы теории графов

Цель работы

1) познакомиться с основными понятиями теории графов;

2) рассмотреть основные операции с графами;

3) научиться решать задачи теории графов средствами Excel.

Теоретическое введение

Основные понятия и определения

Теоретико-множественное определение графа. Пусть V непустое множество, например, 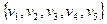. Запишем множество всех его двухэлементных подмножеств V⁽²⁾. Для нашего примера это множество

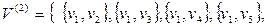
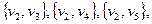
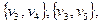
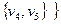
Возьмем произвольно некоторое 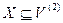, например,

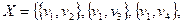
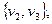
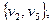
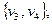
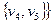
Пара 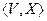называется неориентированным графом, если V – непустое множество элементов, а Х – множество неупорядоченных пар различных элементов из V.

Элементы множества V называются вершинами. Каждую пару x из множества X называют ребром и говорят, что x соединяет вершины u, v 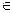V. В таком случае мы будем писать x= u v и говорить, что u и v смежные вершины. Графически ребра принято изображать отрезками линий (не обязательно прямых), а вершины – точками на концах отрезка (см. рис. 4.1).

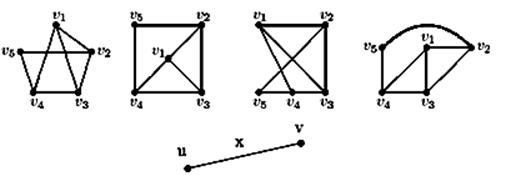
Рис. 4.1 Ребро х и смежные вершины u, v

Про вершину u и ребро x говорят, что они инцидентны. Вершина v и ребро x также инцидентны. Если ребра инцидентны одной вершине, то они называются смежными.

Если ребро ориентировано, то оно называется дугой. Ребро вида x= u u называется петлей. На рис. 4.2 приведены примеры дуги и петли.

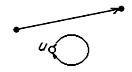
Рис. 4.2 Дуга и петля

Неориентированное ребро называется звеном. Униграф − это такой граф, в котором любые две его вершины соединены не более чем одним ребром. Мультиграф − это такой граф, в котором не допускаются петли, но пары вершин могут соединяться более чем одним ребром (см. рис. 4.3).

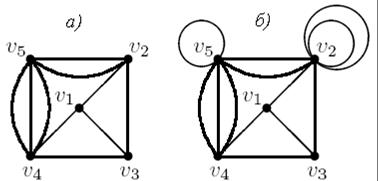
Рис. 4.3 а) мультиграф; б) псевдограф

Если допускаются петли и кратные ребра, то такой граф называется псевдографом.

Орграф − это граф, состоящий из конечного непустого множества вершин V и заданного набора X ориентированных ребер. В орграфе нет петель и кратных дуг.

Граф, не содержащий дуг (ориентированных ребер), называют неориентированным графом или неорграфом.

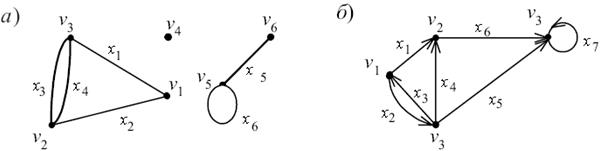
Рис. 4.4 а) неориентированный граф; б) ориентированный граф

Степенью вершины v называется число ребер, инцидентных v. При этом петли считаются дважды. Степень вершины обозначается deg(v). Вершина v изолирована, если deg(v) =0 и концевая, если deg(v) =1. Ребро, инцидентное концевой вершине, также называют концевым. Список степеней всех вершин называют степенной последовательностью графа. Так как каждое ребро инцидентно двум вершинам, то в сумму степеней вершин графа каждое ребро вносит двойку.

Важнейшими количественными характеристиками графа являются: число вершин n=|V |, определяющее порядок графа, и число ребер m=|X |. Граф с n вершинами и m ребрами называется (n, m)–графом.

Исторически первой теоремой теории графов является утверждение, принадлежащее Эйлеру и связывающее количество ребер, вершин и их степеней.

Теорема 1 (Эйлера). Сумма степеней вершин графа G равна удвоенному числу его ребер

.

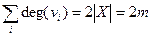Следствие. В конечном графе число вершин нечетной степени четно.

Полный граф − это граф, в котором любые две вершины соединены ребром.

Рис. 4.5 Примеры полных графов

Граф G’(V’, X’) называется подграфом графа G(V, X), есл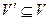и и 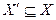. В свою очередь, граф G по отношению к своему подграфу G’ является надграфом.

Если G связный граф, то подграф графа G, у которого 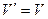и который является деревом, называется остовом графа G.

Рис. 4.6 Все остовные подграфы графа G

Разрез связного графа − это множество ребер, удаление которых приводит к несвязному графу.

Матрицы инциденций и смежности

Пусть дан граф G (V, X),|V|=p, |X|=q.

Матрицей инциденций графа G называется p x q матрица B={b_ij}, элементы которой определяются по формуле

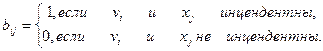
Дата добавления: 2015-07-21