Читайте также:
|
Розглянемо визначення монтажних напружень на прикладі вище проаналізованої стержневої системи. Припустимо, що перший стержень виготовлений коротшим на величину 
. Після зборки системи виникають реактивні зусилля, а тверде тіло займе проміжне положення 
(рис. 2.4).
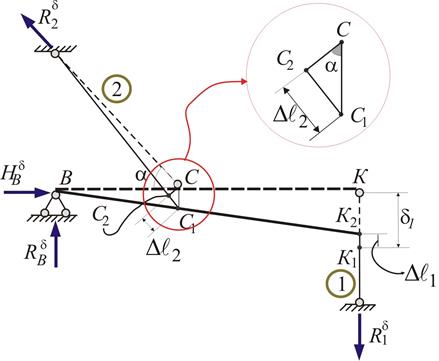
Рис.2.4. Деформована схема
З аналізу деформованої схеми (рис. 2.4) випливає, що стержні подовжуються, в них виникають розтягуючі зусилля 
та 
, у шарнірно нерухомій опорі виникають реакці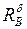ї 
і 
.
Враховуючи метод перерезів внутрішні зусилля виражаються через реактивні 
та 
.
ССЗ.
(2.13)
(2.14)
. (2.15)
2.ГСЗ.
З подоби трикутників 
і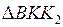 
маємо:
.
З огляду на те, що
, 
,
,
, одержуємо:
.
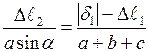Тоді рівняння спільності переміщень приймає вигляд:
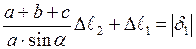(2.16)
3.ФСЗ. З огляду на закон Гука у формі: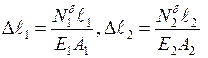 
та, підставляючи ці рівняння в умову (2.16), одержуємо
(2.17)
4.Аналіз.
Вирішуючи спільно рівняння (2.17) і (2.15), маємо:
(2.18)
Поздовжня сила визначається з рівняння (2.15).
Монтажні напруження обчислюємо за формулами:
, 
У випадку коли перший стержень виготовлений довшим, чим це потрібно (
), розрахункові схемі залишаються ідентичними, але зусилля та напруження будуть стискаючими.
Дата добавления: 2015-07-20; просмотров: 114 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Приклад 4. Розрахунок стержньової системи при силовому навантаженні | | | Приклад 6. Визначення температурних напружень в стержньовій системі |